Фрактал — это геометрический объект, характеризующийся наличием структуры, повторяющейся на разных масштабах. В некотором роде, это бесконечный узор. Таким образом, на Рис. 1 изображён фрактал плоскости. Этот термин был предложен Бенуа Мандельбротом в 1975 году. Он происходит от латинского слова fractus, что означает «разбитый» или «растрескавшийся».

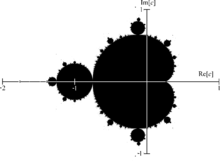
К сожалению, на сегодняшний день не существует строго формального определения фрактала, которое было бы полностью удовлетворительным. Однако можно перечислить некоторые свойства, которые принято ожидать от фрактала:

• Что он самоподобен или, по крайней мере, квази-самоподобен, в смысле Салливана. Например, можно сказать, что фрактал плоскости — это кривая, которая бесконечно повторяет себя.
• Что его топологическая размерность строго меньше его геометрической размерности (или размерности Хаусдорфа). Таким образом, на плоскости можно говорить о «кривых» с бесконечной длиной, несмотря на то, что они находятся в ограниченной области.

Фрактальная структура известна уже давно, хотя использовать её возможности стало возможно только недавно.

Первые идеи, по-видимому, восходят к Готфриду Лейбницу (1646–1716), который рассматривал возможность создания рекурсивно самоподобных объектов. Позже Карл Вейерштрасс (1815–1897) и Нильс Хельге фон Кох (1870–1924) смогли определить функции, графики которых являются фракталами (см. Рис. 2).

В природе часто встречаются объекты с фрактальным видом. Подумайте о деревьях, реках, береговых линиях, облаках и т.д.; см. изображения на Рисунках 3 и 4.

С другой стороны, фрактал можно создать, повторяя простой процесс снова и снова в замкнутом цикле. Например, множество Мандельброта на Рис. 1 определяется комплексными числами c, для которых последовательность {zₙ}, заданная как z₀ = 0 и

zₙ₊₁ = zₙ² + c для n ≥ 0, (1)

остается ограниченной.

Фату, Жюлиа и Мандельброт

Последовательности, порождаемые итерацией комплексных функций, были достаточно подробно изучены Фату и Жюлиа в начале XIX века.

Пьер Жозеф Луи Фату (1878–1929) был французским математиком и астрономом, обучавшимся в École Normale Supérieure в Париже. Он известен, прежде всего, результатами в теории меры, носившими его имя.

Гастон Морис Жюлиа (1893–1978) был французским математиком каталонского происхождения, настоящим пионером в мире фракталов. Он первым объяснил, как можно получить из комплексной функции, посредством итерационного вычисления, множество, границу которого невозможно нарисовать карандашом (так как она имеет бесконечную длину). За это он получил Большую премию по математике от Французской академии наук.

Однако ему не удалось популяризировать свои достижения при жизни. Фракталы стали известны и вызвали интерес только годы спустя, когда информатика помогла их визуализации. Так, стоит упомянуть первые изображения 1978 года, созданные Робертом Бруксом и Питером Мательски, которые были довольно неточными. И, прежде всего, следует учитывать вклад Мандельброта.

Гастон Жюлиа участвовал в Первой мировой войне, где он потерял нос, будучи чуть за двадцать лет. Ему пришлось отказаться от пластической хирургии после нескольких неудачных попыток, и он вынужден был носить небольшую кожаную маску до конца своей жизни.

Бенуа Мандельброт (1924–2010) был польским математиком, ставшим гражданином Франции, а затем США. Без него фракталы не стали бы настолько популярными за столь короткое время. Используя компьютер, он добился точных описаний множества, которое носит его имя, и так называемых множеств Жюлиа, которые, среди прочего, покорили множество творческих людей.

Мандельброт утверждал, что фракталы более естественны (а значит, и более интуитивны), чем объекты, основанные на евклидовой геометрии, которые были созданы (и регуляризированы) искусственно. В подтверждение своей точки зрения он приводил следующую фразу: Облака не являются сферами, горы не являются конусами, береговые линии не являются кругами, кора деревьев не гладкая, и молнии не движутся по прямой линии.

В обучении Мандельброта участвовали несколько великих математиков, которые оказали на него сильное влияние; среди них его дядя Шолем Мандельброjt, Поль Леви в Париже и Джон фон Нейман в Принстоне. После того как он преподавал в университетах Гарварда, Йеля, Парижа и Женевы, в 1958 году он присоединился к IBM Research Center в Нью-Йорке. Там ему поручили конкретную задачу: выявить (и устранить) «шумы», мешающие передаче данных по телефонной линии. Тогда у него возникла блестящая идея принять геометрическую точку зрения, охарактеризовав шум по создаваемым профилям (первая форма визуализации данных). Он быстро понял, что имеет дело с самоподобным явлением: независимо от масштаба, будь то данные за день, час или минуту, шаблон возмущения был удивительно одинаковым.

Таким образом родилась фрактальная геометрия.

Некоторые применения фракталов в наши дни

Область математики, посвящённая описанию и анализу фрактальных множеств, называется фрактальной геометрией. Техники этой области в настоящее время применяются во многих сферах:

Фракталы в астрофизике: Широко распространено мнение, что фрактальная природа межзвёздного газа является ключом к образованию звёзд во Вселенной. Облака частиц (так же как облака в небе) принимают самоподобные профили, связанные с неправильными, но повторяющимися шаблонами, описание которых было бы невозможно без помощи фрактальной геометрии.

Фракталы в биологии: Биологические модели и процессы также характеризуются сосуществованием различных масштабов, с общим шаблоном, который повторяется снова и снова. Например, человеческая хромосома имеет древовидную архитектуру, что позволяет рассматривать её как совокупность «мини-хромосом» и так далее. Последовательности ДНК также демонстрируют самоподобный вид и поведение. Считается, что в недалёком будущем методы фрактальной геометрии помогут точно смоделировать наблюдаемые в природе шаблоны и процессы.

Фракталы в компьютерных науках: В этой области использование фракталов широко распространено. Многие схемы сжатия изображений используют фрактальные алгоритмы для достижения степени сжатия, которая может превышать 75 % от исходного размера. В частности, за последние годы эти методы позволили добиться поистине поразительных художественных достижений, оптических иллюзий, спецэффектов и т.д.

Можно перечислить и многие другие применения. Фракталы являются мощными инструментами для изучения сложных явлений, связанных с коммуникациями (моделирование трафика в сетях), робототехникой, музыкальной композицией, физикой (фазовые переходы в магнетизме), химией (агрегация при ограниченной диффузии), геологией (анализ сейсмических шаблонов, моделирование геологических образований, эрозионные процессы), экономикой (анализ фондового рынка и рыночной динамики) и даже математикой (сходимость численных методов).

В качестве последней любопытной детали, немного фрактальной иронии: обратите внимание, как поведение наших политиков повторяется бесконечно на разных уровнях. Официальные заявления партии зачастую провозглашаются снова и снова монотонно, без значительных изменений: сначала высшими руководителями, затем региональными лидерами, потом нашими местными представителями и, часто, обычными новичками.

Некоторые технические детали для самых требовательных читателей

Что такое квази-самоподобие? По определению, в метрическом пространстве (X, d) множество F ⊂ X называется квази-самоподобным (или квази-однородным), если существуют K > 0 и r₀ > 0 такие, что для каждого x ∈ F и любого r ∈ (0, r₀) множество F ∩ B(x; r) является K-квази-изометричным с F, то есть существует функция f: F ∩ B(x; r) ↦ F, обладающая свойством:

1K d(x₁, x₂) ≤ d(f(x₁), f(x₂)) ≤ K d(x₁, x₂) для всех x₁, x₂ ∈ F ∩ B(x; r).

Что такое топологическая размерность множества? В топологическом пространстве топологическая размерность множества G — это наименьшее число n такое, что любое открытое покрытие G имеет уточнённое покрытие со свойством, что каждая точка G принадлежит не более чем n + 1 множеству этого покрытия (если такого n не существует, говорят, что размерность G бесконечна).

Таким образом, топологическая размерность точки (соответственно, кривой, правильной поверхности) равна 0 (соответственно, 1, 2).

Что такое размерность Хаусдорфа множества? В метрическом пространстве (X, d) размерность Хаусдорфа множества G ⊂ X определяется как

dim_H(G) := sup { s : H^s(G) > 0 },

где H^s(G) := lim (δ → 0⁺) H_δ^s(G) (s-мерная мера Хаусдорфа) и

H_δ^s(G) := inf { ∑_i (δ(E_i))^s : G ⊂ ⋃_i E_i, δ(E_i) < δ }.

Что гласит лемма Фату? Если {fₙ} — последовательность неотрицательных измеримых функций, такая что

lim infₙ→∞ ∫ fₙ dμ < ∞

и определить f(x) := lim infₙ→∞ fₙ(x), то f интегрируема, и

lim infₙ→∞ ∫ fₙ dμ ≥ ∫ f dμ.

Как используется фрактальная геометрия для понимания структуры объекта реального мира или, более широко, множества в метрическом пространстве? Пусть G — такое множество. С точки зрения фрактальной геометрии, сложность множества G определяется его фрактальной размерностью (также называемой размерностью Минковского–Булинжанда). Это значение (конечное или нет) не имеет единого определения, но его интерпретация, свойства и выводы, к которым оно приводит, во всех случаях очень схожи. Одно из подходящих определений выглядит следующим образом:

dim_F(G) = lim (ε → 0⁺) (log N_ε(G)) / (log (1/ε)),

где N_ε(G) — минимальное число шаров радиуса ε, необходимых для покрытия множества G. Фрактальная размерность является мерой того, насколько «сложным» может быть самоподобное множество. Известно, что dim_H(G) всегда меньше или равна dim_F(G). Более того (и это, пожалуй, самое важное), во многих случаях, когда анализируется фрактальная сложность множества в нормированном пространстве и dim_H(G) < ∞, можно точно описать элементы G с использованием конечного числа параметров.

Блокчейн — это технология, которая позволяет создавать распределённые базы данных, где информация хранится в виде цепочки «блоков». Каждый блок содержит данные (например, записи транзакций), и после его добавления он становится частью неизменяемой записи, доступной всем участникам сети. Основные принципы блокчейна:

• Децентрализация: Нет единого центрального органа, который контролирует данные. Вместо этого множество компьютеров (нод) по всему миру совместно поддерживают и проверяют информацию.
• Прозрачность и безопасность: Каждая транзакция фиксируется и становится публичной, что делает систему прозрачной. Благодаря криптографическим методам, данные в блоках защищены от подделки.
• Неизменяемость: После добавления блока в цепочку его практически невозможно изменить без согласия большинства участников сети. Это обеспечивает доверие к сохранённой информации.
• Автоматизация процессов: Блокчейн позволяет создавать так называемые «умные контракты» — программы, которые автоматически выполняют условия соглашения без участия посредников.

Эта технология уже используется в финансовых системах, для создания криптовалют, а также в других областях — от логистики до здравоохранения — для обеспечения прозрачности и безопасности обмена данными. Если вы только начинаете знакомиться с блокчейном, представьте его как цифровой журнал, который постоянно обновляется и проверяется множеством независимых пользователей, обеспечивая доверие и надежность хранимой информации.

Токен — это цифровой актив, который представляет собой определённые права или ценность в рамках проекта. В нашем случае токены выпускаются для поддержки развития виртуальной вселенной. Владение токенами позволяет участникам проекта стать частью эксперимента, получать вознаграждения за свой вклад и наблюдать, как их поддержка способствует эволюции системы. Токены можно обменивать, дарить или хранить в качестве цифрового актива, связанного с ростом и достижениями проекта.

Токен проекта станет неотъемлемой частью экосистемы и будет использоваться для вознаграждения донаторов. Распределение токенов будет осуществляться пропорционально взносам каждого участника, что создаст систему справедливого распределения долей.

Краудфандинг и Экономическая Модель: Финансирование проекта планируется через краудфандинг, что сделает его доступным широкой аудитории, интересующейся эволюцией, симуляцией жизни и блокчейн-технологиями. Токены, полученные в обмен на взносы, дадут участникам определенные привилегии и доступ к уникальным функциям проекта, включая ранний доступ к результатам симуляции и возможность участия в её настройке и развитии.

Использование Токенов для Голосования и Управления: Владельцы токенов могут использовать их для голосования по ключевым вопросам развития проекта, таким как выбор параметров симуляции, расширение функционала или внедрение новых технологий. Это создаст децентрализованную структуру управления, которая позволит сообществу активно участвовать в эволюции проекта.

Привлечение Вычислительных Мощностей через Токенизацию: Токены могут использоваться для стимулирования участников, предоставляющих свои вычислительные мощности. Это будет выгодно тем, кто хочет внести свой вклад в развитие проекта, но не может сделать финансовый взнос. За предоставленные ресурсы они будут получать вознаграждение в виде токенов, что поможет проекту оставаться устойчивым и эффективным.

Долгосрочные Вознаграждения и Участие в Результатах: Участники проекта, поддержавшие его на этапе краудфандинга, смогут получать вознаграждения по мере развития симуляции. Например, если проект начнет генерировать данные или результаты, которые могут быть использованы для научных исследований, обучающих курсов или коммерческих применений, владельцы токенов смогут участвовать в распределении части доходов от этих результатов.