Un fractal es un objeto geométrico caracterizado por presentar una estructura que se repite a diferentes escalas. En cierto modo, se trata de un patrón sin fin. Así, la Figura 1 muestra un fractal del plano. El término fue propuesto por Benoît Mandelbrot en 1975. Proviene del latín fractus, cuyo significado es quebrado o fracturado.

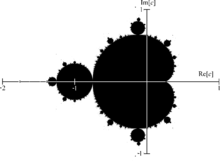
Desgraciadamente, no existe al día de hoy una definición rigurosa de fractal totalmente satisfactoria. Sin embargo, sí pueden enumerarse algunas propiedades que cabe esperar en un fractal:

• Que sea autosimilar o, al menos, quasi-autosimilar, en el sentido de Sullivan. Por ejemplo, en términos vagos se puede decir que un fractal del plano es una curva que se reproduce a sí misma indefinidamente.
• Que su dimensión topológica sea estrictamente inferior a su dimensión geométrica (o dimensión de Hausdorff). Así, en el plano podríamos hablar de «curvas» de longitud infinita, a pesar de estar contenidas en un recinto acotado.

La estructura fractal ha sido reconocida desde hace mucho tiempo, aunque sólo recientemente ha sido posible sacarle partido.

Las primeras ideas parecen remontarse a Gottfried Leibniz (1646-1716), que consideró la posibilidad de generar objetos recursivamente autosimilares. Karl Weierstrass (1815-1897) y Niels Helge von Koch (1870-1924) consiguieron más tarde definir funciones cuyos grafos son fractales (véase la Figura 2).

En la Naturaleza aparecen con frecuencia objetos con apariencia fractal. Pensemos en árboles, ríos, perfiles de costa, nubes, etc.; véanse las imágenes mostradas en las Figuras 3 y 4.

Por otro lado, un fractal puede ser generado repitiendo un proceso simple una y otra vez en un ciclo realimentado. Por ejemplo, el conjunto de Mandelbrot  de la Figura 1 está dado por los números complejos cc tales que la sucesión {zn}{zn} definida por z0=0z0=0 y

zn+1=z2n+c  para n≥0,(1)zn+1=zn2+c  para n≥0,(1)

está acotada.

Fatou, Julia y Mandelbrot

Las sucesiones generadas por iteración de funciones complejas fueron estudiadas con cierta profundidad por Fatou y Julia a principios del siglo XIX.

Pierre Joseph Louis Fatou (1878-1929) fue un matemático y astrónomo francés, formado en la École Normale Supérieure de París. Es conocido, sobre todo, por el resultado de teoría de la medida que lleva su nombre.

Gaston Maurice Julia (1893-1978) fue un matemático francés, de origen catalán, un genuino pionero en el mundo de los fractales. Fue el primero en explicar cómo se puede conseguir a partir de una función compleja, por evaluación iterada, un conjunto cuya frontera es imposible trazar con un lápiz (por ser de longitud infinita). Recibió por ello el Gran Premio de Matemáticas de la Academia de Ciencias Francesa.

Sin embargo, no consiguió popularizar sus logros en vida. Los fractales se hicieron conocidos y ganaron interés sólo años más tarde, cuando la informática ayudó a su representación. Así, cabe mencionar unas primeras imágenes de 1978, de Robert Brooks y Peter Matelski, poco precisas. Y, sobre todo, hay que tener en cuenta las aportaciones de Mandelbrot.

Gaston Julia luchó en la primera guerra mundial, donde perdió la nariz con poco más de veinte años. Se vio obligado a renunciar a la cirugía plástica tras varios intentos fallidos, teniendo que llevar una pequeña máscara de cuero el resto de su vida.

Benoît Mandelbrot (1924-2010) fue un matemático polaco nacionalizado francés y después estadounidense. Sin él, los fractales no habrían llegado a ser tan populares en tan poco tiempo. Incorporando el uso del ordenador, consiguió descripciones precisas del conjunto que lleva su nombre y de los llamados conjuntos de Julia que, entre otras cosas, enamoraron a multitud de creadores artísticos.

Mandelbrot sostenía que los fractales eran más naturales (y por tanto más intuitivos) que los objetos basados en la Geometría Euclídea, que habían sido generados (y regularizados) artificialmente. Como muestra de su punto de vista, he aquí una frase: Las nubes no son esferas, las montañas no son conos, las costas no son círculos, y las cortezas de los árboles no son lisas, ni los relámpagos viajan en una línea recta.

En la formación de Mandelbrot intervinieron varios grandes matemáticos que le influyeron intensamente; entre otros, su tío Szolem Mandelbrojt y Paul Lévy en París y John Von Neumann en Princeton. Tras ser profesor en las universidades de Harvard, Yale, París y Ginebra, se incorporó en 1958 al Centro IBM de Nueva York. Allí le fue encargada una tarea concreta: identificar (y eliminar) los «ruidos» que perturbaban la transmisión de datos por vía telefónica. Tuvo entonces la genial idea de adoptar un punto de vista geométrico, caracterizando el ruido en función de los perfiles generados (una primitiva forma de llevar a cabo visualización de datos). Rápidamente comprendió que estaba en presencia de un fenómeno autosimilar: independientemente de la escala, tanto si los datos representados correspondían a un período de un día, una hora o un minuto, el patrón de la perturbación producida era sorprendentemente el mismo.

De este modo nació la Geometría Fractal.

Algunas aplicaciones de los fractales en los tiempos que corren

La rama de las Matemáticas dedicada a la descripción y análisis de conjuntos fractales se denomina Geometría Fractal. Las técnicas de este área se aplican en la actualidad en muchos ámbitos:

Fractales en Astrofísica: Es comúnmente aceptada la idea de que la naturaleza fractal del gas interestelar es la clave de la formación de las estrellas en el universo. Las nubes de partículas (al igual que las nubes del cielo) adoptan perfiles autosimilares ligados a patrones irregulares pero recurrentes, cuya descripción sería imposible sin la ayuda de la Geometría Fractal.

Fractales en Biología: Los modelos y procesos biológicos también están caracterizados por la coexistencia de escalas diferentes, con un patrón general que se repite una y otra vez. Por ejemplo, un cromosoma humano posee una arquitectura de tipo árbol, que permite concebirlo como un agregado de «mini-cromosomas» y así sucesivamente. Las cadenas de ADN también exhiben aspecto y comportamiento autosimilares. Se cree que, en un futuro no muy lejano, las técnicas de la Geometría Fractal ayudarán a modelar correctamente los patrones y procesos observados en la Naturaleza.

Fractales en Ciencias de la Computación: En este ámbito, la presencia y el uso de fractales están muy extendidos. Muchos esquemas de compresión de imágenes usan algoritmos fractales para conseguir reducciones que pueden ser superiores a un 75 % del tamaño original. En particular, las técnicas han permitido estos últimos años avances artísticos, ilusiones ópticas, efectos especiales, etc. verdaderamente sorprendentes.

Se pueden enumerar muchas más aplicaciones. Los fractales son herramientas de gran potencia para afrontar el estudio de fenómenos complejos relacionados con las comunicaciones (modelado del tráfico en redes), la Robótica, la composición musical, la Física (transiciones de fase en magnetismo), la Química (agregación por difusión limitada), la Geología (análisis de patrones sísmicos, modelado de formaciones geológicas, fenómenos de erosión), la Economía (análisis bursátil y de mercado) e incluso las Matemáticas (convergencia de métodos numéricos).

Como curiosidad final, un poco de ironía fractal: obsérvese cómo los comportamientos de nuestros políticos se repiten sin cesar a distintos niveles. Las declaraciones oficiales de un partido suelen ser proclamadas una y otra vez machaconamente, sin cambios significativos, primero por los más altos dirigentes, después por los líderes regionales, a continuación por nuestros representantes locales y, muchas veces, por los clásicos advenedizos.

Algunos detalles técnicos para los lectores más exigentes

¿Qué es la cuasi-autosimilitud? Por definición, en un espacio métrico (X,d)(X,d), un conjunto F⊂XF⊂X es quasi-autosimilar (o quasi-autosemejante) si existen K>0K>0 y r0>0r0>0 tales que, para cada x∈Fx∈F y cada r∈(0,r0)r∈(0,r0), el conjunto F∩B(x;r)F∩B(x;r) es KK-quasi-isométrico a FF, es decir, existe f:F∩B(x;r)↦Ff:F∩B(x;r)↦F con la propiedad de que

1Kd(x1,x2)≤d(f(x1),f(x2))≤Kd(x1,x2)∀x1,x2∈F∩B(x;r).1Kd(x1,x2)≤d(f(x1),f(x2))≤Kd(x1,x2)∀x1,x2∈F∩B(x;r).

¿Qué es la dimensión topológica de un conjunto? En un espacio topológico, la dimensión topológica de un conjunto GG es el menor nn tal que todo recubrimiento abierto de GG posee un refinamiento con la propiedad de que cada punto de GG pertenece a lo más a n+1n+1 conjuntos del mismo (si un tal nn no existe, se dice que la dimensión de GG es infinito).

De este modo, la dimensión topológica de un punto (resp. una curva, una superficie regular) es 00 (resp. 11, 22).

¿Qué es la dimensión de Haussdorf de un conjunto? En un espacio métrico (X,d)(X,d), la dimensión de Hausdorff de un conjunto G⊂XG⊂X es

dimH(G):=sup{s:Hs(G)>0},dimH⁡(G):=sup{s:Hs(G)>0},

donde Hs(G):=limδ→0+Hsδ(G)Hs(G):=limδ→0+Hδs(G) (la medida de Hausdorff ss-dimensional) y

Hsδ(G):=inf{∑iδ(Ei)s:G⊂⋃iEi,  δ(Ei)<δ}.Hδs(G):=inf{∑iδ(Ei)s:G⊂⋃iEi,  δ(Ei)<δ}.

¿Qué dice el Lema de Fatou? Si {fn}{fn} es una sucesión de funciones medibles no negativas tal que

lim infn→∞∫fndμ<∞lim infn→∞∫fndμ<∞

y ponemos f(x):=lim infn→∞fn(x)f(x):=lim infn→∞fn(x), entonces ff es integrable y

lim infn→∞∫fndμ≥∫fdμ.lim infn→∞∫fndμ≥∫fdμ.

¿Como se usa la Geometría Fractal para comprender la estructura de un objeto del mundo real o, más generalmente, de un conjunto de un espacio métrico? Sea GG este conjunto. Desde el punto de vista de la Geometría Fractal, la complejidad de GG está determinada por su dimensión fractal (también llamada dimensión de Minkowski-Bouligand). Esta cantidad (finita o no) no posee una definición única, pero su interpretación, sus propiedades y  los resultados a los que conduce son en todos los casos muy similares. Una definición adecuada es la siguiente:

dimF(G)=limϵ→0+logNϵ(G)log(1/ϵ),dimF⁡(G)=limϵ→0+log⁡Nϵ(G)log⁡(1/ϵ),

donde Nϵ(G)Nϵ(G) es el mínimo número de bolas de radio ϵϵ que se necesitan para recubrir GG. La dimensión fractal es una medida de lo «complicado» que puede ser  un conjunto autosimilar. Es conocido que dimH(G)dimH⁡(G) es siempre inferior o igual a dimF(G)dimF⁡(G). Por otra parte (y esto es tal vez lo más relevante), en muchos casos de interés, cuando  se está analizando la complejidad fractal de un conjunto de un espacio normado y dimH(G)<∞dimH⁡(G)<∞, es posible describir con precisión los elementos de GG con los valores que toma un número finito de parámetros.

Blockchain es una tecnología que permite crear bases de datos distribuidas, donde la información se almacena en forma de una cadena de «bloques». Cada bloque contiene datos (por ejemplo, registros de transacciones) y, una vez añadido, se convierte en parte de un registro inmutable accesible para todos los participantes de la red.

Los principios básicos de blockchain son:

• Descentralización: No existe una autoridad central que controle los datos. En cambio, múltiples computadoras (nodos) alrededor del mundo colaboran para mantener y verificar la información.
• Transparencia y seguridad: Cada transacción se registra y se vuelve pública, lo que hace que el sistema sea transparente. Gracias a métodos criptográficos, los datos en los bloques están protegidos contra manipulaciones.
• Inmutabilidad: Una vez que un bloque se añade a la cadena, es prácticamente imposible modificarlo sin el consenso de la mayoría de los participantes de la red, lo que garantiza la confianza en la información almacenada.
• Automatización de procesos: Blockchain permite crear «contratos inteligentes», programas que ejecutan automáticamente las condiciones de un acuerdo sin necesidad de intermediarios.

Esta tecnología ya se utiliza en sistemas financieros para la creación de criptomonedas y en otros campos —desde la logística hasta la salud— para garantizar la transparencia y seguridad en el intercambio de datos. Si recién comienzas a conocer blockchain, imagínalo como un registro digital que se actualiza constantemente y es verificado por numerosos usuarios independientes, asegurando la confianza y fiabilidad de la información almacenada.

¿Qué es un Token?

Un token es un activo digital que representa ciertos derechos o valor dentro de un proyecto. En nuestro caso, los tokens se emiten para apoyar el desarrollo del universo virtual. Poseer tokens permite a los participantes del proyecto ser parte del experimento, recibir recompensas por sus contribuciones y ver cómo su apoyo impulsa la evolución del sistema. Los tokens se pueden intercambiar, regalar o mantener como un activo digital vinculado al crecimiento y los logros del proyecto.

El token del proyecto se convertirá en una parte integral del ecosistema y se utilizará para recompensar a los donantes. La distribución de los tokens se realizará de manera proporcional a las contribuciones de cada participante, creando así un sistema de distribución justa de las participaciones.

Crowdfunding y Modelo Económico:
El financiamiento del proyecto se llevará a cabo a través de crowdfunding, lo que lo hará accesible a una audiencia amplia interesada en la evolución, la simulación de la vida y las tecnologías blockchain. Los tokens obtenidos a cambio de las contribuciones otorgarán a los participantes privilegios específicos y acceso a funciones exclusivas del proyecto, incluyendo acceso anticipado a los resultados de la simulación y la posibilidad de participar en su configuración y desarrollo.

Uso de Tokens para Votación y Gobernanza:
Los propietarios de tokens podrán usarlos para votar sobre cuestiones clave en el desarrollo del proyecto, como la elección de parámetros de simulación, la expansión de funcionalidades o la implementación de nuevas tecnologías. Esto creará una estructura de gobernanza descentralizada que permitirá a la comunidad participar activamente en la evolución del proyecto.

Atracción de Potencias Computacionales a través de la Tokenización:
Los tokens se utilizarán para incentivar a los participantes que ofrezcan sus recursos computacionales. Esto será beneficioso para aquellos que deseen contribuir al desarrollo del proyecto pero no puedan hacer una aportación financiera. A cambio de los recursos proporcionados, recibirán recompensas en forma de tokens, lo que ayudará a mantener el proyecto sostenible y eficiente.

Recompensas a Largo Plazo y Participación en los Resultados:
Los participantes del proyecto que lo apoyaron en la etapa de crowdfunding podrán recibir recompensas a medida que se desarrolle la simulación. Por ejemplo, si el proyecto comienza a generar datos o resultados que puedan ser utilizados en investigaciones científicas, cursos educativos o aplicaciones comerciales, los propietarios de tokens podrán participar en la distribución de una parte de los ingresos generados por estos resultados.