Universo Virtual: La idea principal es crear una simulación que modele la emergencia de la vida a partir de materia inanimada y su evolución hasta alcanzar un nivel de inteligencia artificial fuerte. Esto se puede profundizar añadiendo el concepto de multiverso, donde cada universo individual evoluciona bajo diferentes leyes, permitiendo observar trayectorias de desarrollo diversas.
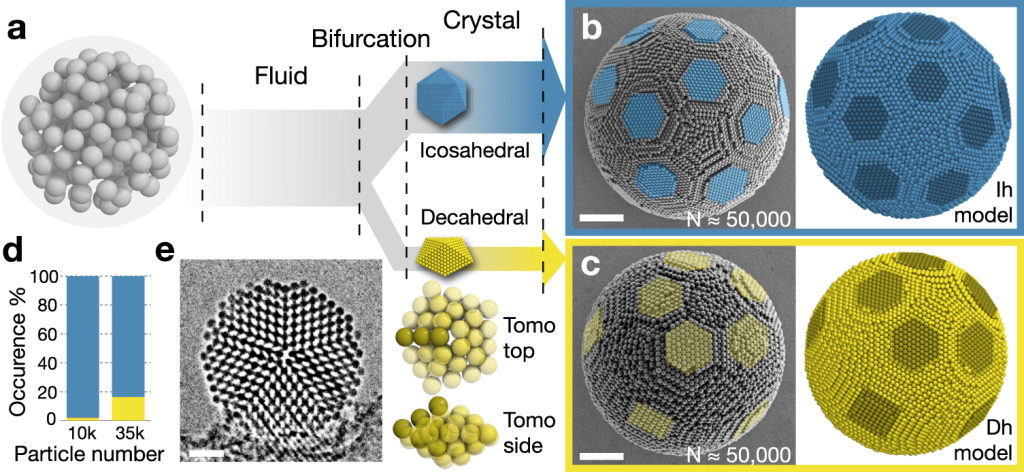
Principios Emergentes: La simulación debe contener los principios fundamentales que sustentan la vida e incluir un mecanismo donde estructuras complejas puedan surgir de elementos simples. La emergencia será el aspecto clave, ya que solo a través de ella se puede lograr una evolución natural. Además, es necesario tener en cuenta el desarrollo de atractores a nivel atómico, lo que permitirá modelar estructuras predecibles sin necesidad de programación estricta.
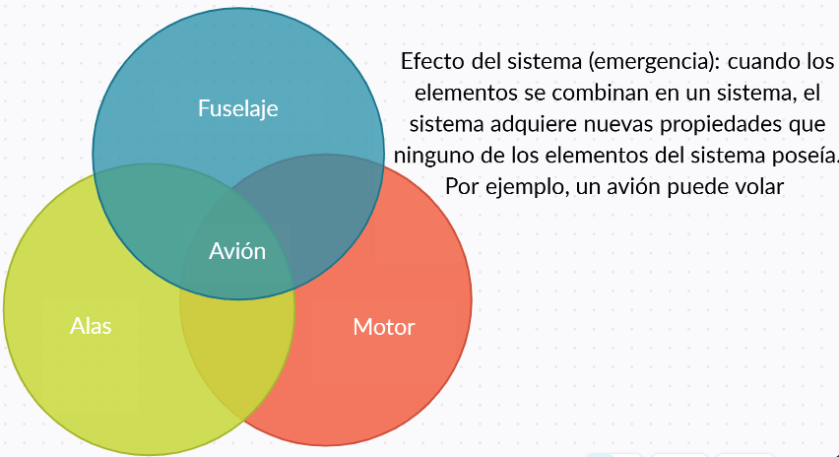
Uso de las Matemáticas como Base: En lugar de simular interacciones atómicas clásicas, se pueden utilizar fórmulas matemáticas y operaciones numéricas para modelar la evolución. Este enfoque permite simplificar y acelerar los cálculos sin perder realismo. También abre la posibilidad de introducir nuevas «leyes de la física» en la simulación, lo que puede conducir a resultados inesperados e interesantes.

Geometría Fractal y Auto-Similitud: La introducción de estructuras auto-similares, como en la naturaleza, permitirá que el sistema se auto-organice en varios niveles, desde moléculas hasta organismos. La auto-similitud puede fomentar una organización más eficiente y estable dentro de la simulación, reflejando patrones naturales de crecimiento y evolución.

Cálculos Paralelos y Blockchain: Para garantizar el funcionamiento estable y seguro del sistema, se propone una infraestructura distribuida utilizando blockchain y cálculos paralelos. De esta forma, es posible aprovechar recursos de todo el mundo, asegurando la disponibilidad de recursos y la confiabilidad del sistema.

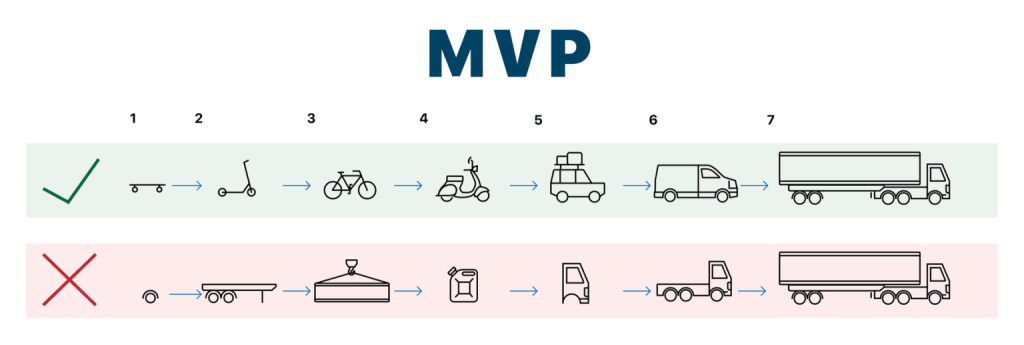
Prototipo como MVP: Para demostrar el potencial del concepto, es importante crear un prototipo que muestre los principios básicos de funcionamiento y emergencia. Un MVP puede consistir en un conjunto pequeño de reglas y sistemas simples que evolucionan e interactúan, permitiendo observar cómo de ellos emerge una estructura más compleja.
Interactividad: Se puede permitir a los usuarios intervenir en la simulación, añadiendo nuevos parámetros y afectando la evolución para observar cómo las diferentes condiciones alteran la trayectoria del desarrollo de la vida. Esto podría convertir el proyecto en una plataforma educativa.

Comunidad científica: El desarrollo de una plataforma abierta para investigaciones puede atraer a científicos y desarrolladores que podrán agregar sus ideas, experimentos y contribuir al desarrollo del proyecto.

Creación de un Token para Fomentar el Apoyo: El token del proyecto será una parte integral del ecosistema y se utilizará para premiar a los donantes. La distribución de los tokens se realizará de manera proporcional a las contribuciones de cada participante, creando un sistema de distribución justa de las participaciones.

Crowdfunding y Modelo Económico: El financiamiento del proyecto se planea a través de crowdfunding, lo que lo hará accesible a un público amplio interesado en la evolución, la simulación de la vida y las tecnologías blockchain. Los tokens obtenidos a cambio de las contribuciones otorgarán a los participantes privilegios específicos y acceso a funciones únicas del proyecto, incluyendo acceso temprano a los resultados de la simulación y la posibilidad de participar en su configuración y desarrollo.

Uso de Tokens para Votación y Gobernanza: Los poseedores de tokens podrán utilizarlos para votar en cuestiones clave sobre el desarrollo del proyecto, como la elección de los parámetros de simulación, la expansión de funcionalidades o la implementación de nuevas tecnologías. Esto creará una estructura descentralizada de gobernanza que permitirá a la comunidad participar activamente en la evolución del proyecto.

Atracción de Poder de Cálculo a través de la Tokenización: Los tokens pueden utilizarse para incentivar a los participantes que proporcionen sus recursos de cálculo. Esto será beneficioso para aquellos que deseen contribuir al proyecto pero no puedan hacer una donación financiera. A cambio de proporcionar recursos, recibirán tokens como recompensa, lo que ayudará al proyecto a mantenerse sostenible y eficiente.

Recompensas a Largo Plazo y Participación en los Resultados: Los participantes que apoyaron el proyecto en la fase de crowdfunding recibirán recompensas a medida que se desarrolle la simulación. Por ejemplo, si el proyecto comienza a generar datos o resultados que pueden ser utilizados para investigaciones científicas, cursos educativos o aplicaciones comerciales, los poseedores de tokens podrán participar en la distribución de parte de los ingresos generados por esos resultados.

Apoyo a la Seguridad y Resiliencia de la Red: Blockchain permitirá que el proyecto mantenga un alto nivel de seguridad de datos y protección contra ataques externos, ya que el sistema será distribuido y resistente a cambios.

1. Sistema Evolutivo Simple:
Elementos Principales del MVP
1. Sistema Evolutivo Simple:
- Conjunto Mínimo de Reglas: El principio emergente principal consistirá en la existencia de «organismos» o «partículas» básicas que puedan interactuar entre sí, desarrollándose en estructuras más complejas. El MVP incluirá un número limitado de reglas simples que definan el comportamiento de los elementos, para observar cómo de ellas se forman «seres» más complejos.
- Selección Evolutiva: La simulación incluirá un mecanismo básico de selección que permitirá que solo «sobrevivan» y «evolucionen» aquellas estructuras que posean ciertas ventajas, como ocurre en la evolución real.
2. Bloques Numéricos y Matemáticos en lugar de Partículas Físicas:
- Modelos Numéricos para Química y Física: Dado que el proyecto utiliza matemáticas en lugar de átomos, el MVP incluirá modelos en los que los valores numéricos representarán las propiedades e interacciones de las partículas. Por ejemplo, los «clústeres» numéricos pueden tener una «energía» o «masa» que influirá en sus interacciones.
- Modelo Simple de Estructuras Complejas: A partir de operaciones numéricas se pueden crear análogos de compuestos químicos, como las «moléculas», que serían agregados de números buscando alcanzar estados estables.


3. Visualización y Animaciones Simples:
- Visualización 2D o 3D: Para la fase inicial, se podrá utilizar una visualización simple que muestre la interacción de «partículas» y la formación de estructuras estables. Incluso formas elementales como puntos o líneas pueden utilizarse para mostrar las relaciones entre las partes del sistema.
- Animación de Cambios Evolutivos: A través de la visualización del cambio gradual de las estructuras, se podrá observar cómo los sistemas simples comienzan a adquirir orden o incluso complejidad.
4. Integración mínima con blockchain:
- Seguimiento de contribuciones y tokens: Para el MVP, basta con crear un contrato inteligente básico en la blockchain que rastree las contribuciones de los participantes y emita tokens proporcionales a las aportaciones.
- Modelo básico de participación de la comunidad: En el MVP se puede introducir un mecanismo simple de votación para los poseedores de tokens sobre cuestiones relacionadas con la evolución de la simulación (por ejemplo, el cambio de una de las reglas básicas).

5. Métricas y análisis:
- Indicadores de desarrollo del sistema: El MVP debe incluir un conjunto básico de métricas para evaluar el «éxito» de la simulación, como el número de interacciones, la estabilidad de las estructuras y la velocidad de desarrollo. Esto permitirá observar cómo aumenta la complejidad y la emergencia a medida que avanza la simulación.
- Análisis de los pasos evolutivos: El sistema puede registrar momentos clave de la evolución, como la formación de una nueva estructura estable o un cambio significativo. Estos datos ayudarán a evaluar la rapidez y eficacia con que el sistema avanza hacia una organización más compleja.
Fases y objetivos del MVP
- Fase 1: Modelado de elementos numéricos y sus interacciones.
- Fase 2: Visualización de interacciones y animación básica.
- Fase 3: Integración con la blockchain para rastrear las contribuciones y distribuir tokens.
- Fase 4: Añadir análisis y métricas para evaluar el desarrollo del sistema.
Estas funciones básicas ayudarán a demostrar los principios de funcionamiento y el potencial del sistema, creando una base para su futura expansión.
Modelos Matemáticos Principales para la Simulación de la Vida
1. Autómatas Celulares:
- Descripción: Los autómatas celulares (AC) son modelos discretos en los cuales el espacio se divide en celdas, cada una de las cuales puede estar en diferentes estados. Estos estados se actualizan según los vecinos, de acuerdo con reglas predefinidas.
- Aplicación en la simulación: Los AC pueden ser útiles para modelar formas elementales de interacción. Por ejemplo, el modelo «Vida» de Conway muestra cómo reglas simples llevan a la creación de estructuras estables, patrones móviles e incluso «organismos». Esto puede ser la base para modelar la aparición de «vida» en tu simulación.


- Ventajas: Los autómatas celulares son adecuados para modelar comportamientos emergentes, y son fácilmente escalables y visualizables.
2. Sistemas de Ecuaciones Diferenciales:
- Descripción: Las ecuaciones diferenciales permiten describir cómo cambian las magnitudes en el tiempo o en el espacio. Por ejemplo, los sistemas de ecuaciones de Lotka-Volterra, que modelan la interacción entre depredadores y presas, pueden dar una analogía para modelar la selección evolutiva.
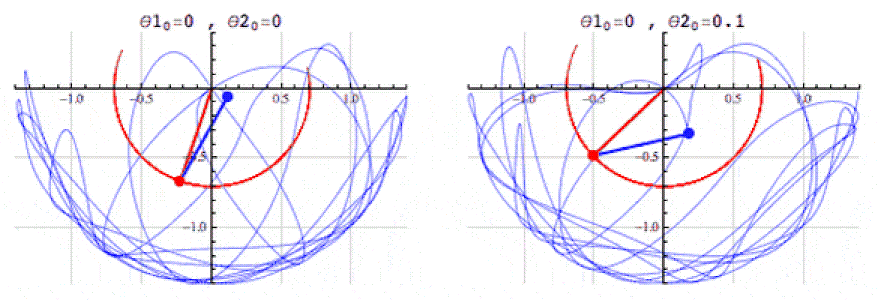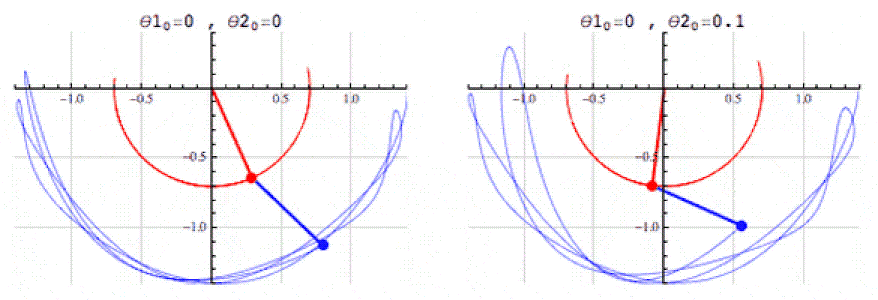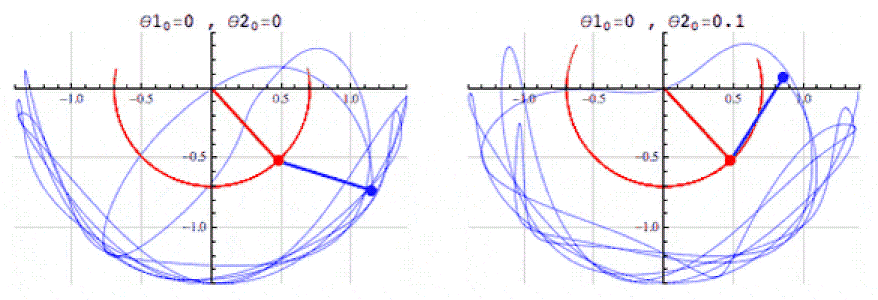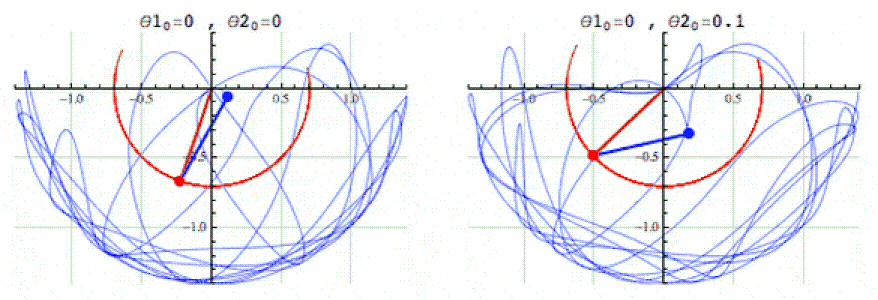

- Aplicación en la simulación: El uso de tales ecuaciones puede describir interacciones entre grupos numéricos que se comportan como especies en un ecosistema. Por ejemplo, los «sistemas» numéricos pueden aumentar o disminuir dependiendo de la «competencia» y los «recursos», lo que agregará realismo a la simulación de la evolución.
- Ventajas: Las ecuaciones diferenciales ayudan a modelar interacciones complejas, como el crecimiento, la adaptación, la «selección natural» y otros procesos dinámicos.
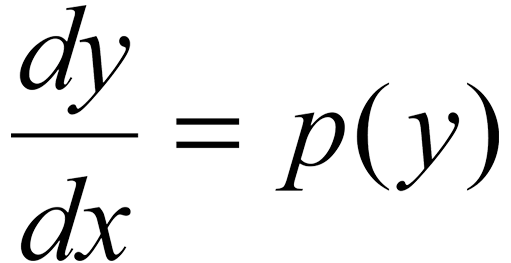

3. Geometría fractal:
- Descripción: Los fractales son estructuras que poseen auto-similitud en diferentes escalas. Por ejemplo, los modelos basados en fractales pueden reproducir estructuras biológicas como árboles, pulmones, vasos sanguíneos y otros sistemas ramificados.
- Aplicación en la simulación: Los algoritmos fractales pueden usarse para crear estructuras estables y auto-similares. Esto asegurará la formación de «organismos» biológicos compuestos de unidades más pequeñas y otorgará a las estructuras la estabilidad inherente a los procesos naturales.


- Ventajas: La autosimilitud y el ahorro de recursos computacionales, ya que los fractales permiten construir estructuras complejas a partir de algoritmos simples, lo que los hace ideales para modelar la evolución.
4. Paseos aleatorios y modelos probabilísticos:
- Descripción: Los paseos aleatorios describen un proceso en el que cada paso está determinado por la aleatoriedad. Este es un modelo común para describir muchos procesos biológicos y físicos.


- Aplicación en la simulación: El uso de paseos aleatorios puede aplicarse para modelar mutaciones, variaciones y cambios. Por ejemplo, los cambios aleatorios en los valores numéricos imitarán las mutaciones en el código genético, lo que puede conducir a cambios evolutivos.
- Ventajas: Los modelos probabilísticos agregan aleatoriedad y variabilidad, imitando el proceso evolutivo en el que las mutaciones aleatorias juegan un papel crucial en la selección natural.

5. Atractores y teoría del caos:
- Descripción: Los atractores son los estados a los que un sistema tiende en su comportamiento a largo plazo. Un ejemplo es el atractor extraño de Lorentz, que modela sistemas complejos con elementos de caos.
- Aplicación en simulación: Los atractores pueden convertirse en una parte importante del modelo evolutivo, donde los «organismos» o estructuras comienzan a evolucionar hacia estados más estables. Esto promoverá la aparición de estructuras estables y, posiblemente, sistemas similares a organismos que evolucionan hacia estados de equilibrio.

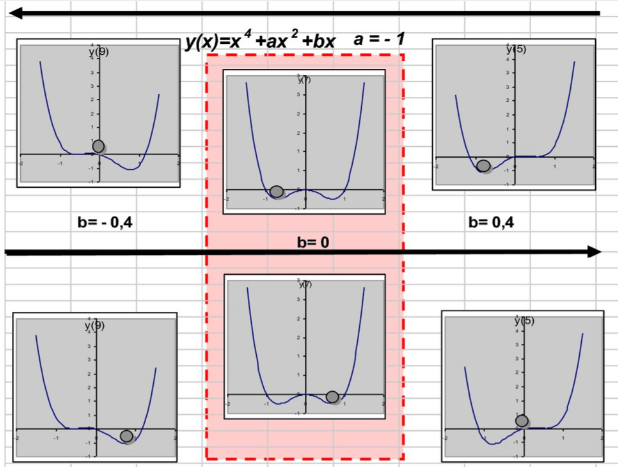
- Ventajas: Los atractores añaden estabilidad y emergencia al sistema, mostrando un comportamiento complejo.
Implementación de Modelos en la Práctica
- Combinación de modelos: Se pueden usar autómatas celulares como el modelo principal para interacciones locales, añadiendo ecuaciones diferenciales para describir cambios a un nivel más global.
- Integración de la geometría fractal: Le dará al sistema una estructura que naturalmente se repetirá y se complicará.
- Mutaciones aleatorias: Introducir un elemento de aleatoriedad para agregar imprevisibilidad y estimular la evolución.
- Análisis de atractores estables: A medida que el sistema se vuelve más complejo, se pueden rastrear los atractores que muestran estados estables hacia los cuales el sistema tiende. Esto permitirá evaluar cómo evolucionan las estructuras estables.
Estos modelos permitirán construir un sistema en el que, a partir de números simples y reglas, comienzan a surgir formas complejas y predecibles de vida.
Bifurcación en la Simulación de la Evolución y Desarrollo de Estructuras
1. Fundamentos de la Bifurcación:
- Descripción: La bifurcación es un punto en el espacio paramétrico en el que un sistema cambia bruscamente su comportamiento. El sistema puede pasar de un estado estable a otro, o mostrar un comportamiento caótico. Un ejemplo clásico es el goteo de agua de un grifo, donde las gotas inicialmente caen de manera uniforme, pero luego comienzan a formar pares.
- Aplicación en evolución: En la simulación, la bifurcación puede utilizarse para modelar cambios drásticos, como mutaciones o saltos en el desarrollo. Por ejemplo, una estructura puede pasar de un estado de crecimiento estable a ramificarse o descomponerse en elementos más pequeños, como ocurre en los sistemas vivos.
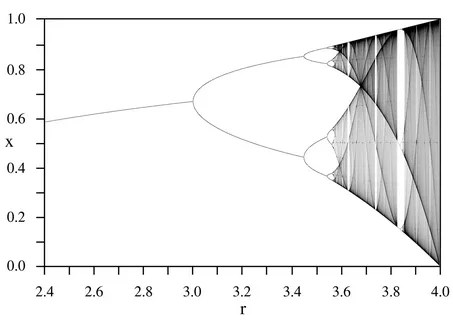

2. Modelado de Transiciones Críticas:
- Transformaciones Evolutivas: La bifurcación será útil en la modelización de formas de vida que enfrentan «transiciones críticas» o «barreras evolutivas». Tales momentos pueden incluir la aparición de nuevos tipos de estructuras o funciones.
- Momentos de Innovación y Ramificación: Por ejemplo, cuando una estructura determinada alcanza su límite, puede bifurcarse, creando nuevos tipos o subestructuras. Esto modelará los procesos naturales de diversificación y adaptación.

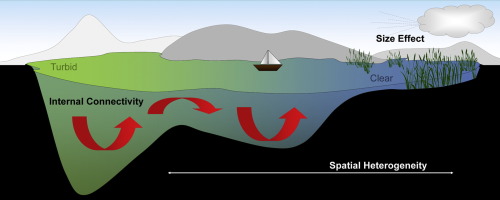
3. Bifurcación en Sistemas Numéricos Simples:
- Modelos Numéricos: En la práctica, la bifurcación se puede implementar mediante modelos en los que pequeños cambios en los parámetros conducen a cambios drásticos en el comportamiento del sistema. Por ejemplo, si en un sistema numérico ocurren pequeños desplazamientos de valores, esto puede causar una transición de la estructura de un estado estable a otro.
- Condiciones para la Aparición de la Bifurcación: Condiciones matemáticas o umbrales específicos pueden actuar como disparadores de bifurcaciones, lo que agregará un nivel adicional de complejidad e imprevisibilidad a su modelo.

4. Aplicación para la Simulación de Procesos Reales:
- Comportamiento Emergente: Las bifurcaciones pueden dar lugar a nuevas estructuras o comportamientos que inicialmente no fueron programados en el sistema. Esto agregará una sensación de evolución viva, donde los cambios ocurren de manera abrupta y conducen a nuevos niveles de organización.
- Caminos Evolutivos: Dado que la bifurcación puede crear nuevas formas estables, nuestra simulación podrá demostrar cómo diferentes «organismos» o estructuras se desarrollan a lo largo de diversas trayectorias.

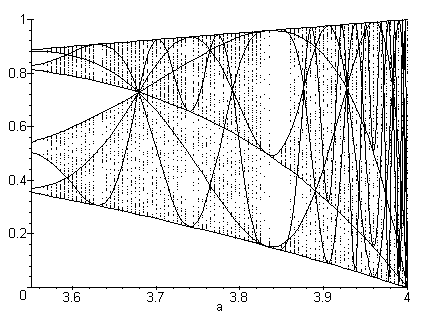
5. Análisis y Visualización de Diagramas de Bifurcación:
- Visualización Gráfica: Se pueden crear diagramas de bifurcación para mostrar los cambios en los parámetros. Esto permitirá visualizar cómo las estructuras pasan de un estado a otro y proporcionará una representación clara de los «puntos de ramificación» de la evolución.
- Utilidad para Pruebas: Los diagramas de bifurcación pueden servir como una herramienta para analizar diferentes escenarios en la simulación, ayudando a identificar las «ramificaciones» más interesantes que merecen ser investigadas más a fondo.

Así, la bifurcación añadirá imprevisibilidad y cambios «escalonados» a la simulación, haciendo que el proceso evolutivo sea más realista y dinámico. Esto permitirá que la simulación siga diversos caminos evolutivos, enriqueciendo su contenido y añadiendo otro nivel de emergencia.
Resonancia en la Simulación Evolutiva
1. Fundamentos de la Resonancia:
- Descripción: La resonancia es un fenómeno en el cual un sistema comienza a oscilar con mayor amplitud bajo la influencia de una fuerza externa, si la frecuencia de la fuerza coincide con la frecuencia natural del sistema. Esta propiedad se manifiesta en sistemas naturales y artificiales, y puede amplificar o atenuar las oscilaciones.
- Aplicación en la Simulación: La resonancia se puede utilizar para modelar eventos en los que una estructura u organismo alcanza un «estado resonante», lo que conduce a cambios bruscos, como la amplificación de señales, el crecimiento de estructuras o la aparición de nuevas propiedades.
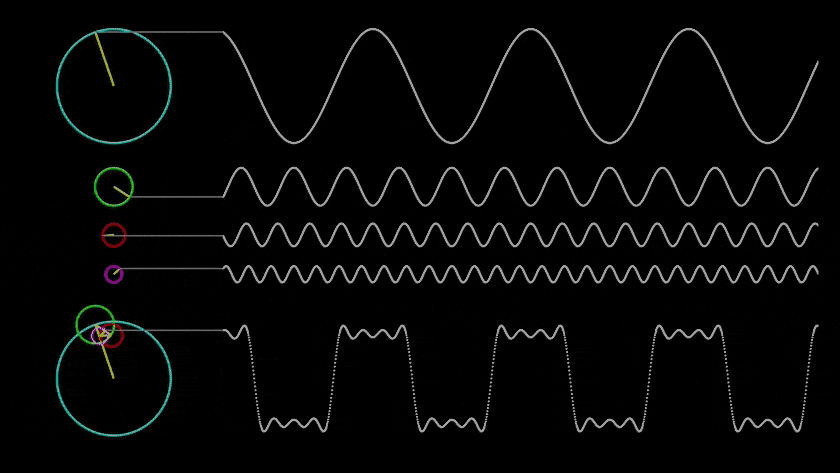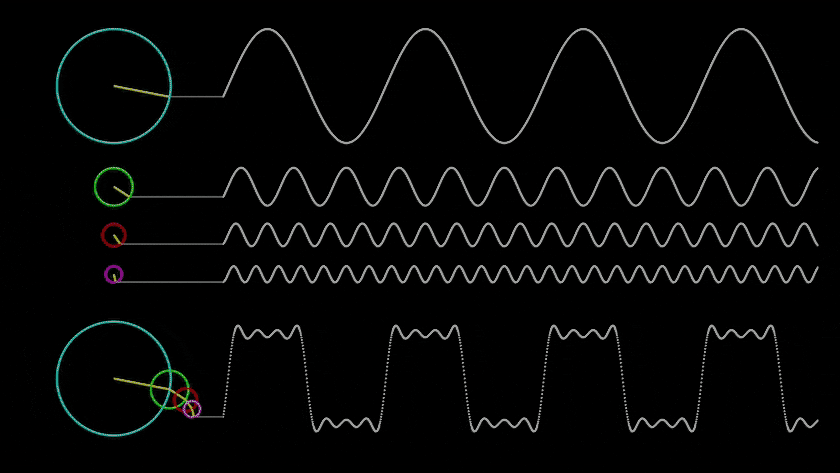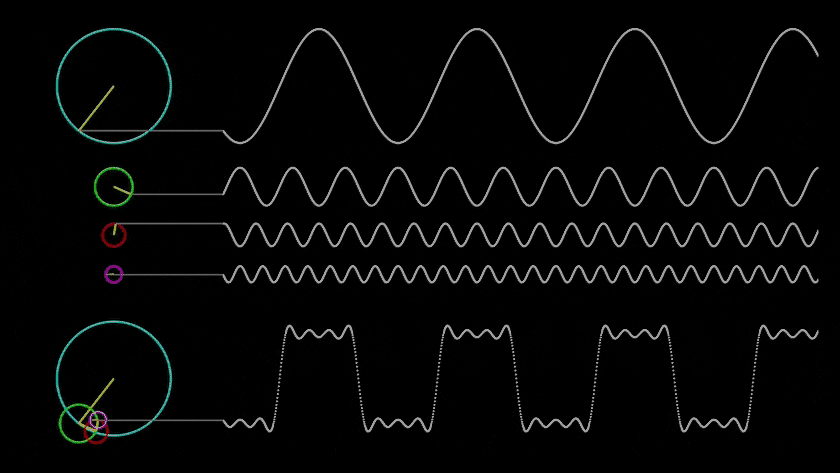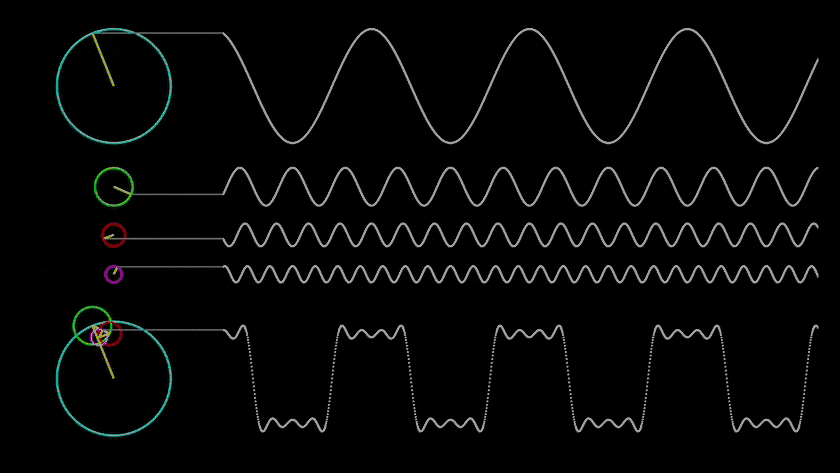
2. Resonancia como Factor de Aceleración de los Cambios Evolutivos:
- Aplicación en la evolución: En el proceso evolutivo, la resonancia puede servir como catalizador para los cambios. Por ejemplo, un sistema numérico, estando en un estado «resonante», puede pasar rápidamente a una estructura más compleja, ya que la amplitud de sus interacciones aumentará.
- Modelado de Mutaciones y Adaptaciones: Se puede introducir un parámetro en el que las frecuencias resonantes conduzcan a la intensificación de los cambios en el «código genético» de los organismos simulados, favoreciendo la aparición de adaptaciones y mutaciones, como ocurre bajo la influencia de factores externos en biología.

3. Conexión con las Bifurcaciones y Puntos Críticos:
- Transiciones entre estados: La resonancia puede conducir a bifurcaciones, donde el sistema se desvía de un estado estable y pasa a un nuevo camino evolutivo. Esto es especialmente útil para modelar situaciones en las que los cambios se acumulan gradualmente, pero la transición a un nuevo estado ocurre bruscamente bajo la influencia de condiciones resonantes.
- Creación de estructuras dinámicas: En el estado de resonancia, la simulación puede mostrar la formación de estructuras oscilantes, similares a los ritmos biológicos, como el latido del corazón o las oscilaciones en las cadenas nerviosas.


4. Efecto de resonancia en sistemas numéricos:
- Ciclos resonantes: En el modelo numérico, se pueden introducir ciclos donde la resonancia conduce a la intensificación de las interacciones, creando reacciones en cadena. Estos ciclos pueden incluir «ondas» energéticas que se propagan a través del sistema, creando nuevas estructuras estables.
- Sistemas oscilantes y ritmos: La resonancia puede formar ritmos regulares en los modelos numéricos, que serán la base para simular procesos vitales, como los ritmos biológicos o los procesos respiratorios.


5. Análisis y visualización de transiciones resonantes:
- Visualización de estados de resonancia: Se pueden mostrar los puntos de resonancia y los modos oscilatorios a través de gráficos de amplitudes o energías. Esto permitirá observar visualmente cómo los estados de resonancia forman o modifican estructuras.
- Evaluación del impacto de la resonancia en la evolución: Analizando las transiciones de resonancia, se podrá evaluar cómo los estados de resonancia afectan la velocidad de la evolución, la formación de nuevas estructuras y el progreso general del sistema.

De este modo, la resonancia permitirá modelar cambios periódicos y amplificados que surgen bajo la influencia de fuerzas externas e internas. Esto aportará una nueva dinámica a la simulación, permitiéndole mostrar un comportamiento más realista e impredecible relacionado con los procesos de resonancia.
Autosimilitud en el proyecto
1. Creación de estructuras autosimilares
- Idea: En lugar de modelar cada partícula o estructura individualmente, se pueden usar algoritmos fractales para crear grandes estructuras que incluyan automáticamente los detalles necesarios.
- Ejemplo: En lugar de modelar cada átomo en un árbol, una estructura fractal puede describir la forma general de las ramas y hojas, estableciendo reglas generales de crecimiento, lo que reduce la necesidad de calcular cada partícula individual.
- Ventaja: Esto permitirá simplificar el modelado de objetos complejos y sistemas biológicos, ya que las grandes estructuras fractales se pueden generar a partir de reglas matemáticas simples y repeticiones, ahorrando así recursos computacionales.
2. Jerarquía de Niveles Fractales
- Principio de jerarquía: El sistema puede dividirse en varios niveles de estructuras auto-similares, comenzando desde partículas elementales hasta grandes estructuras biológicas.
- Técnica de implementación: En el primer nivel están las partículas elementales, que se agrupan en clústeres o celdas en el segundo nivel. Estos clústeres luego se combinan en estructuras más grandes, formando el tercer nivel y así sucesivamente. Cada nivel sigue reglas fractales, donde las interacciones de las partículas dentro de un nivel están sujetas a reglas simplificadas, y las interacciones entre niveles se reducen a un pequeño conjunto de parámetros clave.
- Ventaja: Esta estructura permite simular en diferentes escalas sin necesidad de calcular cada nivel en detalle al mismo tiempo.
3. Algoritmos Recursivos para Interacciones
- Algoritmos basados en recursión: Las interacciones pueden codificarse a través de algoritmos recursivos que describen el comportamiento de los sistemas en cada nivel, desde partículas elementales hasta estructuras de alto nivel.
- Ventajas: Mediante recursión se pueden establecer reglas para las interacciones en cada nivel del sistema, y los algoritmos pueden auto-sostenerse, creando estructuras dinámicas y estables. Esto reduce el volumen de cálculos necesarios, ya que las interacciones generales en niveles más altos pueden modelar sistemas más grandes y complejos.
4. Dinámica Adaptativa de Estructuras Fractales
- Modelado de la evolución: Las estructuras fractales se adaptarán dinámicamente, permitiendo que los «organismos» en la simulación evolucionen y se desarrollen a partir de reglas simples. Si elementos individuales cambian, toda la estructura puede cambiar en consecuencia.
- Ejemplo: Supongamos que una «partícula» comienza a oscilar con una frecuencia específica, su cambio podría afectar a toda la estructura, creando una nueva configuración fractal que imite mutaciones y desarrollo.
- Ventajas: Esto permite modelar estados resonantes, transiciones críticas e incluso bifurcaciones, todo esto se puede incorporar a la dinámica de las estructuras fractales.
5. Cálculo Paralelo para Algoritmos Fractales
- Paralelismo: Dado que las estructuras fractales se basan en la auto-similitud, sus cálculos pueden distribuirse entre varios procesadores. Por ejemplo, cada nodo fractal puede ser procesado independientemente de los demás, lo que permite paralelizar las tareas.
- Ventajas: Gracias a los cálculos paralelos, se pueden procesar millones de partículas simultáneamente, y el sistema seguirá siendo escalable. Se puede utilizar blockchain para coordinar los cálculos distribuidos, de modo que las partículas «sepan» cómo se influyen mutuamente en cada nivel de la simulación.
6. Uso de Sistemas L para el Crecimiento Biológico
- Sistemas L: Son gramáticas formales que describen el crecimiento biológico basado en reglas recursivas y estructuras fractales. Se pueden aplicar para modelar plantas, sistemas nerviosos y otras estructuras biológicas complejas.
- Ventajas: Con ellos, se pueden generar rápidamente estructuras ramificadas y gestionar el proceso de crecimiento sometiéndolo a reglas simples. Esto facilitará la creación de modelos realistas, reduciendo los costos de recursos.
Conclusión
El uso de fractales permitirá crear estructuras jerárquicas auto-similares que se repiten en diferentes niveles y pueden adaptarse dinámicamente. Combinando algoritmos fractales con cálculos paralelos y reglas adaptativas, podremos implementar una simulación escalable que soporte millones de partículas que interactúan entre sí, utilizando blockchain para la coordinación.
