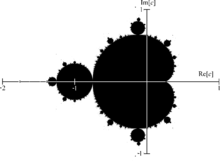
A fractal is a geometric object characterized by having a structure that repeats at different scales. In a way, it is a never-ending pattern. Thus, Figure 1 shows a fractal in the plane. The term was proposed by Benoît Mandelbrot in 1975. It comes from the Latin fractus, meaning broken or fractured.

Unfortunately, to this day there is no fully satisfactory rigorous definition of a fractal. However, some properties that one might expect in a fractal can be enumerated:

• That it is self-similar or at least quasi-self-similar, in the sense of Sullivan. For example, in vague terms one can say that a fractal in the plane is a curve that reproduces itself indefinitely.
• That its topological dimension is strictly lower than its geometric dimension (or Hausdorff dimension). Thus, in the plane we might speak of “curves” of infinite length, even though they are contained within a bounded region.

The fractal structure has been recognized for a long time, although it has only recently been possible to exploit it.

The earliest ideas seem to date back to Gottfried Leibniz (1646-1716), who considered the possibility of generating recursively self-similar objects. Later, Karl Weierstrass (1815-1897) and Niels Helge von Koch (1870-1924) managed to define functions whose graphs are fractals (see Figure 2).

In nature, objects with a fractal appearance frequently occur. Think of trees, rivers, coastlines, clouds, etc.; see the images shown in Figures 3 and 4.

On the other hand, a fractal can be generated by repeating a simple process over and over in a feedback loop. For example, the Mandelbrot set in Figure 1 is given by the complex numbers c such that the sequence {zₙ} defined by z₀ = 0 and

zₙ₊₁ = zₙ² + c  for n ≥ 0, (1)

remains bounded.

Fatou, Julia, and Mandelbrot

The sequences generated by iterating complex functions were studied in some depth by Fatou and Julia in the early 19th century.

Pierre Joseph Louis Fatou (1878-1929) was a French mathematician and astronomer, trained at the École Normale Supérieure in Paris. He is best known for the measure theory result that bears his name.

Gaston Maurice Julia (1893-1978) was a French mathematician of Catalan origin, a genuine pioneer in the world of fractals. He was the first to explain how a set whose boundary is impossible to trace with a pencil (because it is of infinite length) can be obtained from a complex function by iterative evaluation. He received the Grand Prize in Mathematics from the French Academy of Sciences for this work.

However, he did not manage to popularize his achievements during his lifetime. Fractals became known and attracted interest only years later, when computing helped to represent them. Thus, it is worth mentioning some early images from 1978 by Robert Brooks and Peter Matelski, which were somewhat imprecise. And, above all, one must consider Mandelbrot’s contributions.

Gaston Julia fought in World War I, where he lost his nose at just over twenty years old. He was forced to give up plastic surgery after several failed attempts, having to wear a small leather mask for the rest of his life.

Benoît Mandelbrot (1924-2010) was a Polish mathematician who became a French and later American citizen. Without him, fractals would not have become so popular in such a short time. By incorporating the use of the computer, he achieved precise descriptions of the set that bears his name and of the so-called Julia sets, which, among other things, captivated a multitude of artistic creators.

Mandelbrot maintained that fractals were more natural (and therefore more intuitive) than objects based on Euclidean Geometry, which had been artificially generated (and regularized). As evidence of his point of view, here is a phrase: Clouds are not spheres, mountains are not cones, coastlines are not circles, and tree barks are not smooth, nor do lightning bolts travel in a straight line.

In Mandelbrot’s education, several great mathematicians influenced him intensely; among others, his uncle Szolem Mandelbrojt and Paul Lévy in Paris and John Von Neumann in Princeton. After teaching at Harvard, Yale, Paris, and Geneva, he joined the IBM Research Center in New York in 1958. There he was given a specific task: to identify (and eliminate) the «noise» that disturbed data transmission over telephone lines. It was then that he had the brilliant idea of adopting a geometric point of view, characterizing the noise in terms of the profiles generated (an early form of data visualization). He quickly realized that he was in the presence of a self-similar phenomenon: regardless of the scale, whether the represented data corresponded to a period of a day, an hour, or a minute, the pattern of the disturbance produced was surprisingly the same.

This is how Fractal Geometry was born.

Some Applications of Fractals Today

The branch of Mathematics dedicated to the description and analysis of fractal sets is called Fractal Geometry. Techniques from this area are currently applied in many fields:

Fractals in Astrophysics: It is commonly accepted that the fractal nature of interstellar gas is key to the formation of stars in the universe. Clouds of particles (just like clouds in the sky) adopt self-similar profiles linked to irregular but recurring patterns, whose description would be impossible without the help of Fractal Geometry.

Fractals in Biology: Biological models and processes are also characterized by the coexistence of different scales, with a general pattern that repeats over and over. For example, a human chromosome has a tree-like architecture, which allows it to be conceived as an aggregate of “mini-chromosomes” and so on. DNA strands also exhibit a self-similar appearance and behavior. It is believed that in the not-too-distant future, techniques from Fractal Geometry will help accurately model the patterns and processes observed in Nature.

Fractals in Computer Science: In this field, the presence and use of fractals are widespread. Many image compression schemes use fractal algorithms to achieve reductions that can exceed 75% of the original size. In particular, these techniques have enabled, in recent years, artistic advances, optical illusions, special effects, and more that are truly astonishing.

Many more applications can be listed. Fractals are powerful tools for studying complex phenomena related to communications (network traffic modeling), Robotics, musical composition, Physics (phase transitions in magnetism), Chemistry (diffusion-limited aggregation), Geology (seismic pattern analysis, geological formation modeling, erosion phenomena), Economics (stock and market analysis), and even Mathematics (convergence of numerical methods).

As a final curiosity, a bit of fractal irony: observe how the behaviors of our politicians repeat endlessly at different levels. The official statements of a party are often proclaimed repeatedly in a monotonous way, without significant changes, first by the top leaders, then by regional leaders, subsequently by our local representatives, and often by the usual upstarts.

Some Technical Details for the Most Demanding Readers

What is quasi-self-similarity? By definition, in a metric space (X, d), a set F ⊂ X is quasi-self-similar (or quasi-self-similar) if there exist K > 0 and r₀ > 0 such that, for every x ∈ F and every r ∈ (0, r₀), the set F ∩ B(x; r) is K-quasi-isometric to F, that is, there exists a function f: F ∩ B(x; r) ↦ F with the property that

1K d(x₁, x₂) ≤ d(f(x₁), f(x₂)) ≤ K d(x₁, x₂) ∀ x₁, x₂ ∈ F ∩ B(x; r).

What is the topological dimension of a set? In a topological space, the topological dimension of a set G is the smallest n such that every open cover of G has a refinement with the property that each point of G belongs to at most n + 1 sets of the cover (if such an n does not exist, the dimension of G is said to be infinite).

Thus, the topological dimension of a point (resp. a curve, a regular surface) is 0 (resp. 1, 2).

What is the Hausdorff dimension of a set? In a metric space (X, d), the Hausdorff dimension of a set G ⊂ X is defined as

dim_H(G) := sup { s : H^s(G) > 0 },

where H^s(G) := lim₍δ→0⁺₎ H_δ^s(G) (the s-dimensional Hausdorff measure) and

H_δ^s(G) := inf { ∑_i (δ(E_i))^s : G ⊂ ⋃_i E_i, δ(E_i) < δ }.

What does Fatou’s Lemma state? If {fₙ} is a sequence of non-negative measurable functions such that

lim infₙ→∞ ∫ fₙ dμ < ∞

and we define f(x) := lim infₙ→∞ fₙ(x), then f is integrable and

lim infₙ→∞ ∫ fₙ dμ ≥ ∫ f dμ.

How is Fractal Geometry used to understand the structure of a real-world object or, more generally, a set in a metric space? Let G be such a set. From the point of view of Fractal Geometry, the complexity of G is determined by its fractal dimension (also called the Minkowski–Bouligand dimension). This quantity (finite or not) does not have a unique definition, but its interpretation, properties, and the results it leads to are in all cases very similar. An appropriate definition is as follows:

dim_F(G) = lim₍ε→0⁺₎ (log N_ε(G)) / (log (1/ε)),

where N_ε(G) is the minimum number of balls of radius ε required to cover G. The fractal dimension is a measure of how «complicated» a self-similar set can be. It is known that dim_H(G) is always less than or equal to dim_F(G). Moreover (and perhaps most importantly), in many cases of interest, when analyzing the fractal complexity of a set in a normed space with dim_H(G) < ∞, it is possible to accurately describe the elements of G with a finite number of parameters.

Blockchain is a technology that enables the creation of distributed databases where information is stored as a chain of «blocks.» Each block contains data (such as transaction records) and, once added, becomes part of an immutable ledger accessible to all network participants.

The basic principles of blockchain include:

• Decentralization: There is no central authority controlling the data. Instead, multiple computers (nodes) around the world collaborate to maintain and verify the information.
• Transparency and Security: Every transaction is recorded and made public, which makes the system transparent. Cryptographic methods protect the data in each block from tampering.
• Immutability: Once a block is added to the chain, it is nearly impossible to alter without the consensus of the majority of network participants. This ensures trust in the stored information.
• Process Automation: Blockchain enables the creation of “smart contracts” — programs that automatically execute the terms of an agreement without the need for intermediaries.

This technology is already used in financial systems for creating cryptocurrencies and in various other fields—from logistics to healthcare—to ensure transparent and secure data exchange. If you are just beginning to learn about blockchain, think of it as a digital ledger that is constantly updated and verified by many independent users, ensuring the reliability and trustworthiness of the information stored.

What is a Token?

A token is a digital asset that represents certain rights or value within a project. In our case, tokens are issued to support the development of the virtual universe. Owning tokens allows project participants to be part of the experiment, receive rewards for their contributions, and see how their support drives the evolution of the system. Tokens can be exchanged, gifted, or held as a digital asset linked to the project’s growth and achievements.

The project token will become an integral part of the ecosystem and will be used to reward donors. Token distribution will be carried out in proportion to each participant’s contributions, creating a system of fair distribution of shares.

Crowdfunding and Economic Model:
The project will be funded through crowdfunding, making it accessible to a broad audience interested in evolution, life simulation, and blockchain technologies. Tokens received in exchange for contributions will grant participants certain privileges and access to unique project features, including early access to simulation results and the ability to participate in its configuration and development.

Token Use for Voting and Governance:
Token holders can use their tokens to vote on key project development issues, such as choosing simulation parameters, expanding functionality, or implementing new technologies. This will create a decentralized governance structure, enabling the community to actively participate in the project’s evolution.

Attracting Computational Power through Tokenization:
Tokens can be used to incentivize participants who provide their computational resources. This will benefit those who wish to contribute to the project but are unable to make a financial contribution. For the resources provided, they will receive rewards in the form of tokens, helping the project to remain sustainable and efficient.

Long-term Rewards and Participation in Outcomes:
Project participants who support it during the crowdfunding phase will be able to receive rewards as the simulation develops. For example, if the project generates data or results that can be used for scientific research, educational courses, or commercial applications, token holders can participate in the distribution of part of the income generated by these outcomes.