Virtual Universe: The main idea is to create a simulation that models the emergence of life from non-living matter and its evolution into strong artificial intelligence. This can be expanded by adding the concept of multiversality, where each individual universe evolves according to different laws, allowing the observation of various development trajectories.

Emergent Principles: The simulation should incorporate fundamental principles underlying life and include a mechanism through which complex structures can emerge from simple elements. Emergence will be a key aspect, as only through it can natural evolution be achieved. It is also necessary to consider the development of attractors at the atomic level, allowing the modeling of predictable structures without rigid programming.

Using Mathematics as a Foundation: Instead of simulating classical atomic interactions, mathematical formulas and numerical operations can be used to model evolution. This approach simplifies and accelerates computations without losing realism. It also opens up the possibility of introducing new «laws of physics» into the simulation, potentially leading to unexpected and interesting results.

Fractal Geometry and Self-Similarity: Introducing self-similar structures, as seen in nature, will enable the system to self-organize at various levels—from molecules to organisms. Self-similarity also contributes to the formation of stable structures, such as tree branches, landscape reliefs, biological structures, and even neural networks.

Parallel Computing and Blockchain: To ensure the system’s stability and security, a distributed infrastructure utilizing blockchain and parallel computing is proposed. This approach allows computational power to be sourced globally, ensuring resource availability and system reliability.

Prototype as MVP: To demonstrate the potential of the concept, it is important to create a prototype that showcases the fundamental principles of operation and emergence. The MVP may consist of a small set of rules and simple systems that evolve and interact, allowing observation of how more complex structures emerge from them.

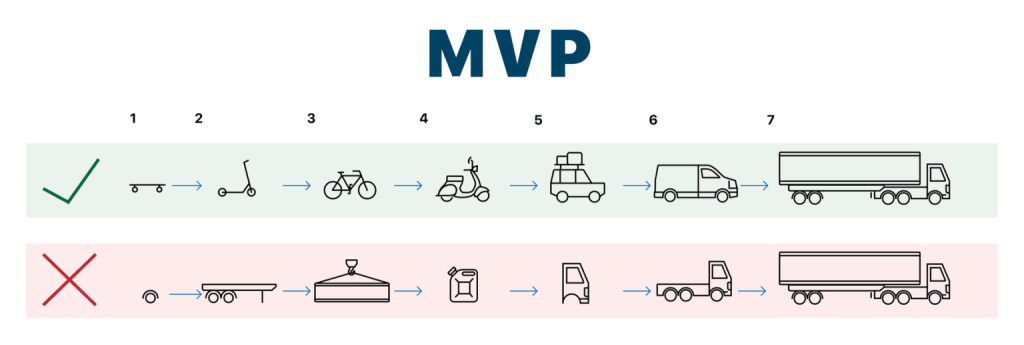
Interactivity: Users can be allowed to intervene in the simulation, adding new parameters and influencing evolution to see how different conditions alter the trajectory of life development. This could turn the project into an educational platform.

Scientific Community: Developing an open research platform can attract scientists and developers who can contribute their ideas, experiments, and advancements to the project.

Creating a Token to Encourage Support: The project token will become an integral part of the ecosystem and will be used to reward donors. Token distribution will be proportional to each participant’s contributions, creating a fair share allocation system.

Crowdfunding and Economic Model: The project will be funded through crowdfunding, making it accessible to a broad audience interested in evolution, life simulation, and blockchain technologies. Tokens received in exchange for contributions will grant participants certain privileges and access to unique project features, including early access to simulation results and the ability to participate in its configuration and development.

Token Usage for Voting and Governance: Token holders can use them to vote on key project development decisions, such as choosing simulation parameters, expanding functionality, or implementing new technologies. This will create a decentralized governance structure that allows the community to actively participate in the project’s evolution.

Attracting Computing Power through Tokenization: Tokens can be used to incentivize participants who provide their computing power. This will benefit those who want to contribute to the project’s development but cannot make a financial donation. In return for their resources, they will receive rewards in the form of tokens, helping the project remain sustainable and efficient.

Long-Term Rewards and Participation in Results: Project supporters who contribute during the crowdfunding stage will be able to receive rewards as the simulation evolves. For example, if the project begins generating data or results that can be used for scientific research, educational courses, or commercial applications, token holders will be able to participate in the distribution of a portion of the revenue from these outcomes.

Supporting Network Security and Resilience: The blockchain will enable the project to maintain a high level of data security and protection against external attacks, as the system will be decentralized and resistant to modifications.

Core Elements of the MVP

1. Simple Evolutionary System:

• Minimal Set of Rules: The main emergent principle will involve basic «organisms» or «particles» that can interact with each other, developing into more complex structures. The MVP will include a limited number of simple rules defining the behavior of elements to observe how more complex «beings» emerge from them.
• Evolutionary Selection: The simulation will include a basic selection mechanism that will allow only those structures with certain advantages to «survive» and «develop,» just as in real evolution.

2. Numerical and Mathematical Blocks Instead of Physical Particles:

• Numerical Models for Chemistry and Physics: Since the project uses mathematics instead of atoms, the MVP will include models where numerical values correspond to the properties and interactions of particles. For example, numerical «clusters» may have certain «energy» or «mass» influencing their interactions.
• Simple Model of Complex Structures: Numerical operations can be used to create analogs of chemical compounds, such as «molecules,» which will be aggregates of numbers striving toward stable states.

3. Visualization and Simple Animations:

• 2D or 3D Visualization: For the initial stage, a simple visualization showing the interaction of «particles» and the formation of stable structures will suffice. Even basic forms like points or lines can be used to represent the relationships between parts of the system.
• Animation of Evolutionary Changes: By visualizing the gradual changes in structures, it will be possible to observe how simple systems start to acquire order or even complexity.

4. Minimal Blockchain Integration:

• Tracking Contributions and Tokens: For the MVP, it will be enough to create a basic smart contract on the blockchain that tracks participants’ contributions and issues tokens proportional to their contributions.
• Basic Community Participation Model: The MVP can introduce a simple voting mechanism for token holders regarding the evolution of the simulation (e.g., changing one of the basic rules).

5. Metrics and Analytics:

• System Development Indicators: The MVP should include a set of basic metrics to assess the «success» of the simulation, such as the number of interactions, stability of structures, and rate of development. This will allow monitoring how the complexity and emergence increase over time during the simulation.
• Analysis of Evolutionary Steps: The system can capture key moments in evolution — when a new stable structure is formed or a significant change occurs. This data will help evaluate how quickly and effectively the system is progressing toward complex organization.

Stages and Goals of the MVP

1. Stage 1: Modeling numerical elements and their interactions.
2. Stage 2: Visualizing interactions and basic animation.
3. Stage 3: Blockchain integration for tracking contributions and distributing tokens.
4. Stage 4: Adding analytics and metrics to assess system development.

These basic functions will help demonstrate the principles of operation and the potential strength of the system, creating a foundation for further expansion.

Key Mathematical Models for Simulating Life

1. Cellular Automata:

• Description: Cellular automata (CA) are discrete models where space is divided into cells, each of which can be in various states. These states are updated based on neighboring cells according to specified rules.

• Application in Simulation: CA can be useful for modeling elementary forms of interaction. For example, Conway’s «Life» model shows how simple rules lead to the creation of stable structures, moving patterns, and even «organisms.» This could serve as a foundation for simulating the emergence of «life» in your simulation.

• Advantages: Cellular automata are well-suited for modeling emergent behavior, and they are easy to scale and visualize.

2. Systems of Differential Equations:

• Description: Differential equations describe how quantities change over time or space. For example, the Lotka-Volterra system of equations, which models the interaction between predators and prey, can provide an analogy for modeling evolutionary selection.

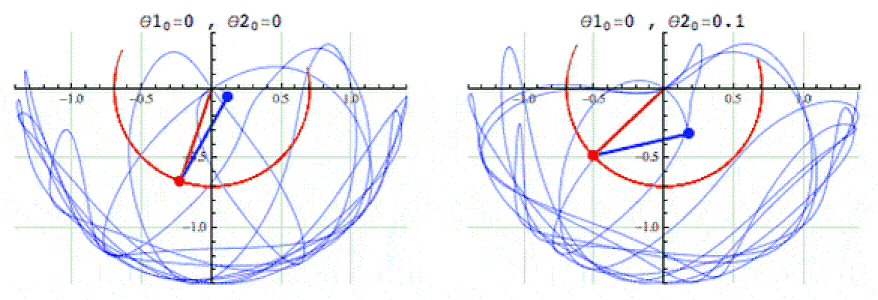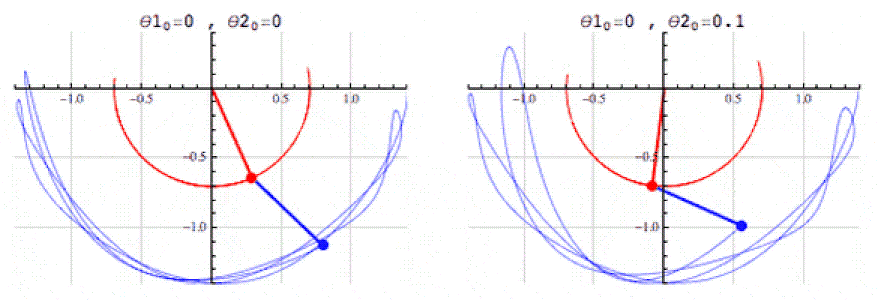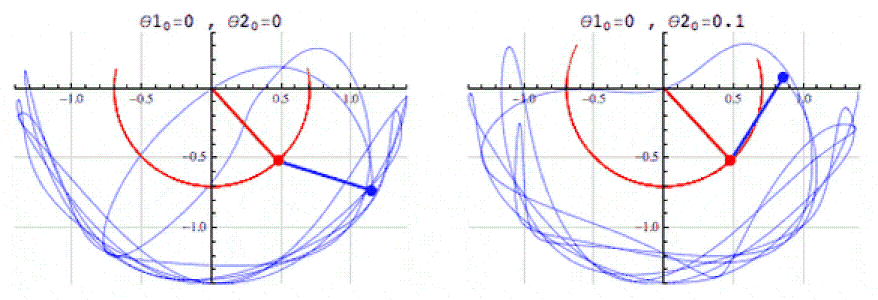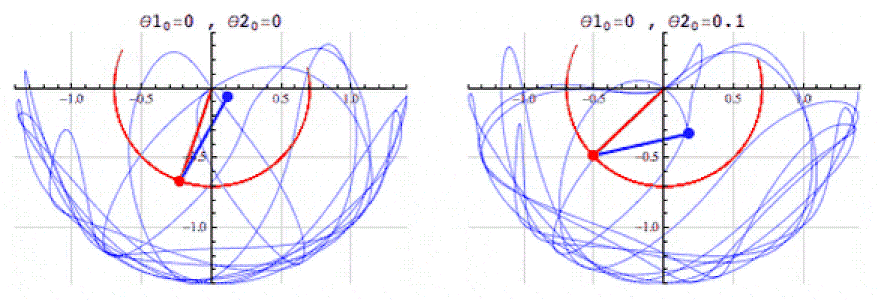
• Application in Simulation: Using such equations can describe interactions between numerical clusters that behave like species in an ecosystem. For example, numerical «systems» may increase or decrease depending on «competition» and «resources,» which adds realism to modeling evolution.

• Advantages: Differential equations will help model complex interactions, such as growth, adaptation, «natural selection,» and other dynamic processes.

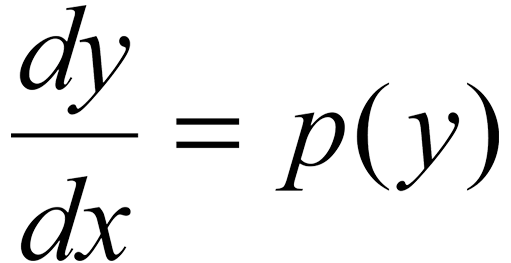
3. Fractal Geometry:

• Description: Fractals are structures that exhibit self-similarity across different scales. For example, models based on fractals can reproduce biological structures such as trees, lungs, blood vessels, and other branching systems.

• Application in Simulation: Fractal algorithms can be used to create stable and self-similar structures. This will ensure the formation of biological «organisms» made up of smaller units and give the structures the resilience characteristic of natural processes.

• Advantages: Self-similarity and computational efficiency, as fractals allow complex structures to be built from simple algorithms, which is ideal for modeling evolution.

4. Random Walks and Probabilistic Models:

• Description: Random walks describe a process where each step is determined by randomness. This is a common model used to describe many biological and physical processes.

• Application in Simulation: Random walks can be used to model mutations, variations, and changes. For example, random changes in numerical values will simulate mutations in the genetic code, which can lead to evolutionary changes.

• Advantages: Probabilistic models add randomness and variability, simulating the evolutionary process where random mutations play a crucial role in natural selection.

5. Attractors and Chaos Theory:

• Description: Attractors are states that a system tends toward in the long-term behavior. An example is the Lorenz strange attractor, which models complex systems with elements of chaos.

• Application in Simulation: Attractors can become an important part of the evolutionary model, where «organisms» or structures begin to evolve towards more stable states. This will facilitate the emergence of stable structures and possibly organism-like systems evolving towards equilibrium states.

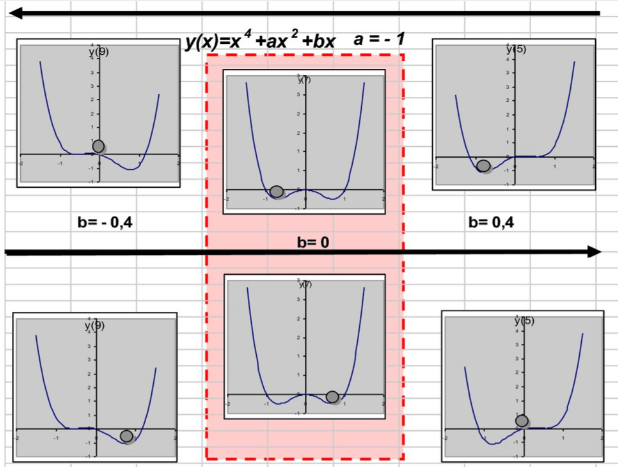
• Advantages: Attractors add a system of stability and emergence, while demonstrating complex behavior.

Implementing Models in Practice

1. Combination of Models: Cellular automata can be used as the primary model for local interactions, adding differential equations to describe changes at a more global level.
2. Integration of Fractal Geometry: This will give the system a structure that naturally repeats and becomes more complex.
3. Random Mutations: Introduce an element of randomness to add unpredictability and stimulate evolution.
4. Analysis of Stable Attractors: As the system becomes more complex, attractors can be tracked to show stable states toward which the system is evolving. This will allow the assessment of how stable structures evolve.

These models will allow the construction of a system where complex and predictable life forms begin to emerge from simple numbers and rules.

Bifurcation in Evolution and Structural Development Modeling

1. Basics of Bifurcation:

• Description: Bifurcation is a point in the parameter space at which a system drastically changes its behavior. The system can transition from one stable state to another or exhibit chaotic behavior. A classic example is water dripping from a tap, where drops initially fall evenly and then begin to form pairs.

• Application in Evolution: In simulation, bifurcation can be used to model sharp changes, such as mutations or jumps in development. For example, a structure can transition from one state of stable growth to branching or breaking into smaller elements, as seen in living systems.

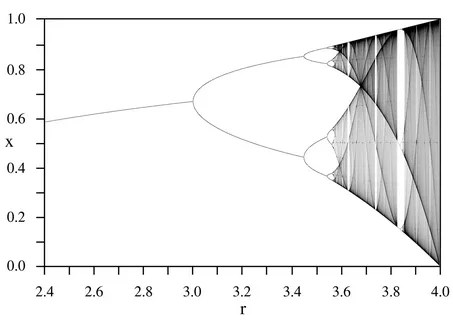
2. Modeling Critical Transitions:

• Evolutionary Transformations: Bifurcation will be useful when modeling life forms that encounter «critical transitions» or «evolutionary barriers.» Such moments may include the emergence of new types of structures or functions.

• Moments of Innovation and Branching: For example, when a particular structure reaches its limit, it may bifurcate, creating new species or substructures. This will model the natural processes of diversification and adaptation.

3. Bifurcation in Simple Numerical Systems:

• Numerical Models: In practice, bifurcation can be implemented through models in which small changes in parameters lead to dramatic changes in the system’s behavior. For example, if small shifts in values occur in a numerical system, it may cause the structure to transition from one stable state to another.

• Conditions for the Emergence of Bifurcation: Certain mathematical conditions or thresholds can serve as triggers for bifurcations, adding an additional layer of complexity and unpredictability to your model.

4. Application for Simulating Real Processes:

• Emergent Behavior: Bifurcations can lead to the emergence of new structures or behaviors that were not initially programmed into the system. This will add a sense of living evolution, where changes occur in leaps and lead to new levels of organization.

• Evolutionary Paths: Since bifurcation can create new stable forms, our simulation will be able to demonstrate how different «organisms» or structures evolve along different trajectories.

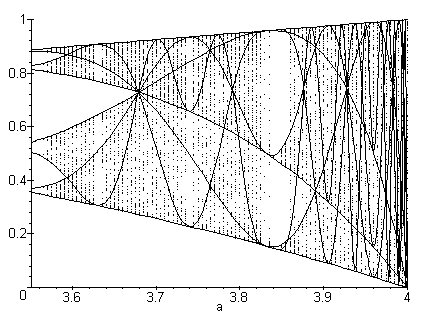
5. Analysis and Visualization of Bifurcation Diagrams:

• Graphical Representation: Bifurcation diagrams can be created to display changes in parameters. This will allow visualization of how structures transition from one state to another and provide a clear view of the «branch points» in evolution.

• Benefits for Testing: Bifurcation diagrams can serve as a tool for analyzing different scenarios in the simulation, helping to identify the most interesting «branches» worth further exploration.

Thus, bifurcation will add unpredictability and «jump-like» changes to the simulation, making the evolutionary process more realistic and dynamic. This will allow the simulation to follow diverse evolutionary paths, enriching it and adding another level of emergence.

Resonance in Evolutionary Simulation

1. Basics of Resonance:

• Description: Resonance is a phenomenon in which a system starts to oscillate with greater amplitude when an external force is applied at the system’s natural frequency. This property occurs in both natural and artificial systems and can amplify or dampen oscillations.

• Application in simulation: Resonance can be used to model events when a structure or organism reaches a «resonant state,» leading to sudden changes — amplifying signals, growing structures, or emerging new properties.

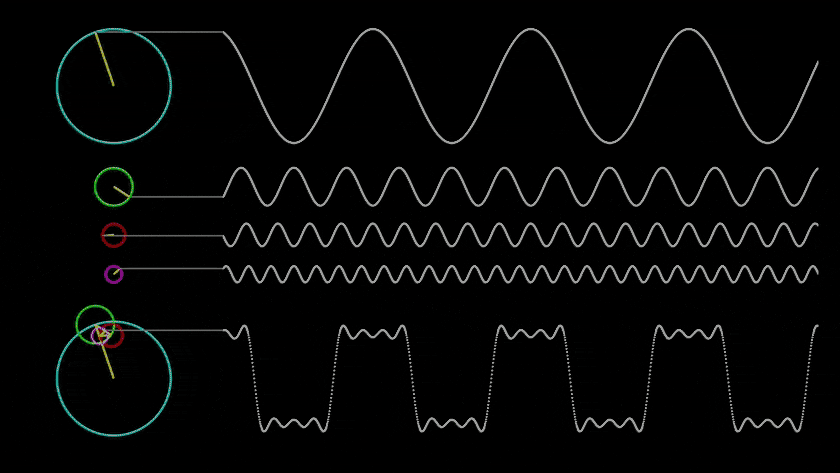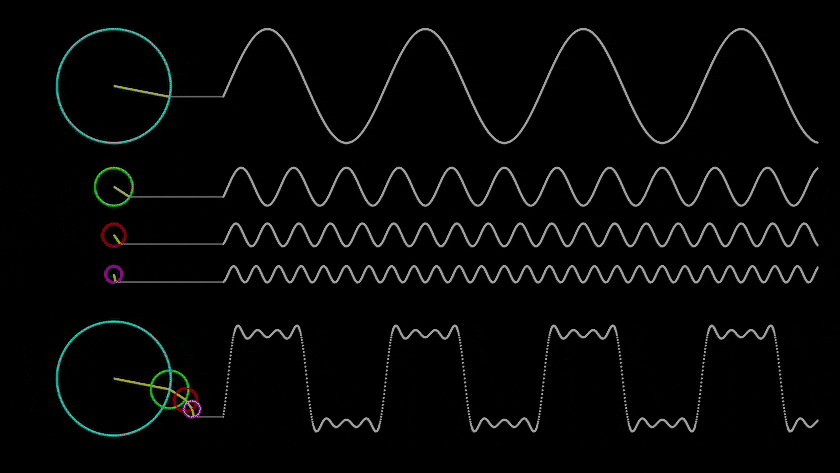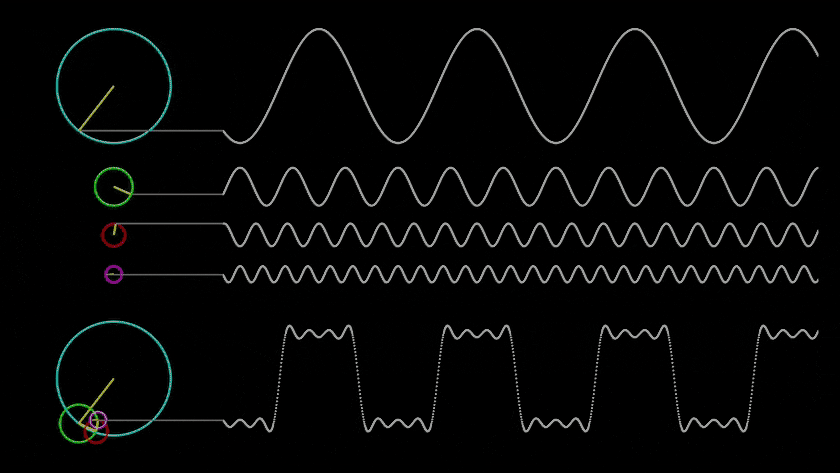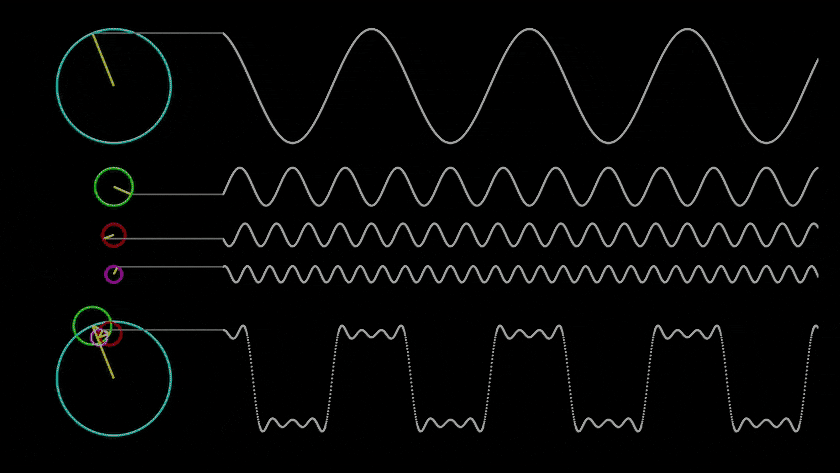
2. Resonance as a Factor of Accelerating Evolutionary Changes:

• Application in Evolution: In the process of evolution, resonance can act as a catalyst for changes. For example, a numerical system in a «resonant» state can quickly transition to a more complex structure, as the amplitude of its interactions will increase.

• Modeling Mutations and Adaptations: A parameter can be introduced in which resonant frequencies lead to the amplification of changes in the «genetic code» of simulated organisms, promoting the appearance of adaptations and mutations, as happens under the influence of external factors in biology.

3. Connection with Bifurcations and Critical Points:

• Transitions Between States: Resonance can lead to bifurcations, where the system deviates from a stable state and transitions to a new evolutionary path. This is especially useful for modeling situations where changes accumulate gradually, but the transition to a new state occurs suddenly under the influence of resonant conditions.

• Creation of Dynamic Structures: In a resonant state, the simulation can demonstrate the formation of oscillatory structures, similar to biological rhythms, such as heartbeats or oscillations in neural circuits.

4. Resonance Effect in Numerical Systems:

• Resonant Cycles: In a numerical model, cycles can be introduced where resonance leads to the amplification of interactions, creating chain reactions. Such cycles may involve energy «waves» that spread through the system, forming new stable structures.

• Oscillatory Systems and Rhythms: Resonance can form regular rhythms in numerical models, which will serve as the foundation for modeling life processes, such as biological rhythms or respiratory processes.

5. Analysis and Visualization of Resonant Transitions:

• Visualization of Resonant States: Resonant points and oscillatory modes can be displayed through amplitude or energy graphs. This will allow for visual observation of how resonant states form or alter structures.

• Assessment of the Impact of Resonance on Evolution: By analyzing resonant transitions, it will be possible to evaluate how significantly resonant states affect the speed of evolution, the formation of new structures, and the overall progress of the system.

Thus, resonance will add the ability to model periodic and amplified changes that arise under the influence of external and internal forces. This will introduce new dynamics into the simulation, allowing it to demonstrate more realistic and unpredictable behavior associated with resonant processes.

Self-Similarity in the Project

1. Creating Self-Similar Structures

• Idea: Instead of modeling each particle or each structure individually, fractal algorithms can be used to create large structures that automatically include the necessary details.
• Example: Instead of modeling every atom in a tree, a fractal structure can describe the overall shape of the branches and leaves by setting general growth rules, reducing the need to calculate each individual particle.
• Advantage: This will simplify the modeling of complex objects and biological systems, as large fractal structures can be generated from simple mathematical rules and repetitions, thus saving computational resources.

2. Hierarchy of Fractal Levels

• Principle of hierarchy: The system can be divided into several levels of self-similar structures, starting from elementary particles and ending with large biological structures.
• Implementation Technique: At the first level — elementary particles that merge into clusters or cells at the second level. These clusters then combine into larger structures, forming the third level, and so on. Each level follows fractal rules, where interactions between particles within a level follow simplified rules, and interactions between levels are reduced to a small set of key parameters.
• Advantage: Such a structure allows for the simulation to be considered at different scales without the need for detailed computation of each level simultaneously.

3. Recursive Algorithms for Interactions

• Recursion-based Algorithms: Interactions can be encoded through recursive algorithms that describe the behavior of systems at each level, starting from elementary particles and ending with high-level structures.
• Advantages: With recursion, rules for interactions at each system level can be defined, and the algorithms will be self-sustaining, creating stable and dynamic structures. This reduces the amount of necessary computation, as general interactions at higher levels can model larger and more complex systems.

4. Adaptive Dynamics of Fractal Structures

• Modeling Evolution: Fractal structures will dynamically adapt, allowing «organisms» in the simulation to evolve and develop based on simple rules. If individual elements change, the entire structure can change accordingly.
• Example: Suppose an individual «particle» begins to oscillate at a certain frequency, its change may affect the entire structure, creating a new fractal configuration that mimics mutations and development.
• Advantages: This provides the ability to model resonant states, critical transitions, and even bifurcation — all of which can be embedded into the dynamics of fractal structures.

5. Parallel Computing for Fractal Algorithms

• Parallelism: Since fractal structures are based on self-similarity, their computations can be distributed across multiple processors. For example, each fractal node can be processed independently from others, allowing for task parallelization.
• Advantages: Thanks to parallel computing, millions of particles can be processed simultaneously, and the system will remain scalable. Blockchain can be used to coordinate distributed computations so that particles «know» how they affect each other at every level of the simulation.

6. Using L-systems for Biological Growth

• L-systems: These are formal grammars that describe biological growth based on recursive rules and fractal structures. They can be applied to model plants, nervous systems, and other complex biological structures.
• Advantages: With them, branching structures can be quickly and efficiently generated, and the growth process can be managed by simple rules. This simplifies the creation of realistic models, reducing resource costs.

Conclusion

The use of fractals will allow the creation of self-similar hierarchical structures that repeat at different levels and can dynamically adapt. By combining fractal algorithms with parallel computing and adaptive rules, we will be able to implement a scalable simulation supporting millions of particles interacting with each other, using blockchain for coordination.